Cho tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và OA = a, O

Cho tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và OA = a, OB = 2a, OC = 3a. Bán kính mặt cầu ngoại tiếp tứ diện O.ABC là:

• A.

  A. $\large a\sqrt{3}$

• B.

  B. $\large \dfrac{3a}{2}$

• C.

  C. $\large \dfrac{a\sqrt{6}}{2}$

• D.

  D. $\large \dfrac{a\sqrt{14}}{2}$

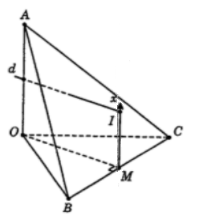
Gọi M là trung điểm BC, suy ra M là tâm đường tròn ngoại tiếp $\large \Delta OBC$.

Kẻ Mx $\large \perp$(OBC) (như hình vẽ)

Suy ra Mx là trục  của $\large \Delta OBC$.

Trong mặt phẳng (OA,Mx), kẻ trung trực d của đoạn thẳng OA cắt Mx tại I.

Khi đó I chính là tâm mặt cầu ngoại tiếp tứ diện.

Bán kính mặt cầu: $\large R = IO = \sqrt{IM^{2}+OM^{2}}= \sqrt{\left ( \dfrac{1}{2}OA \right )^{2}+\left ( \dfrac{1}{2}BC \right )^{2}}= \dfrac{a\sqrt{14}}{2}$ 

Chọn D.