Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc 60∘60∘ . Thể tích của khối cầu ngoại tiếp khối chóp S.ABCD là:
Đáp án án đúng là: D
Lời giải chi tiết:
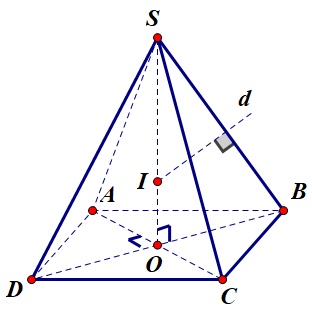
Gọi O=AC∩BDO=AC∩BD, suy ra SO ⊥⊥(ABCD).
Ta có 60∘=(^SB,(ABCD))=(^SB,OB)=^SBO60∘=(ˆSB,(ABCD))=(ˆSB,OB)=ˆSBO
Trong ΔSOBΔSOB, ta có SO=OB.tan^SBO=a√62SO=OB.tanˆSBO=a√62
Ta có SO là trục của hình vuông ABCD.
Trong mặt phẳng SOB, kẻ đường trung trực d của đoạn SB.
Gọi I=SO∩dI=SO∩d
⇒{ I∈SO I∈d⇒{ IA=IB=IC=ID IS=IB⇒IA=IB=IC=ID=IS=R
Xét ΔSBD có { SB=SD ^SBD=^SBO=60∘⇒ΔSBD đều.
Do đó d cũng là đường trung tuyến của ΔSBD. Suy ra I là trọng tâm ΔSBD.
Bán kính mặt cầu R=SI=23SO=a√63.
Suy ra V=43πR3=8πa3√627
Chọn D.
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC = a .
- Cho tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và OA = a, O
- Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a . Mặt phẳng
- Cho hình bình hành ABCD có $\large \widehat{BAD} = \alpha (0^{\circ} <
- Trong các hình nón tròn xoay cùng có diện tích toàn phần bằng $\large