Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC = a .

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên cạnh bên SB và SC. Thể tích của khối cầu tạo bởi mặt cầu ngoại tiếp hình chóp A.HKCB là:

• A.

  A. $\large \dfrac{\sqrt{2}\pi a^{3}}{3}$

• B.

  B. $\large \sqrt{2}\pi a^{3}$

• C.

  C. $\large \dfrac{\pi a^{3}}{6}$

• D.

  D. $\large \dfrac{\pi a^{3}}{2}$

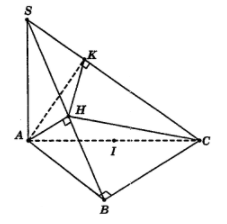
Theo giả thiết, ta có:

$\large \widehat{ABC} = 90^{\circ}$ và $\large \widehat{AKC} = 90^{\circ}$.   (1)

Do $\large \begin{cases}
 & \ AH \perp SB \\ 
 & \ BC \perp AH (BC \perp (SAB))
\end{cases}\Rightarrow AH \perp HC$  (2)

Từ (1) và (2), suy ra ba điểm B, H, K cùng nhìn xuống AC dưới một góc $\large 90^{\circ}$ nên hình chóp A.HKCB nội tiếp mặt cầu tâm I là trung điểm AC, bán kính $\large R = \dfrac{AC}{2} = \dfrac{AB\sqrt{2}}{2} = \dfrac{a\sqrt{2}}{2}$ 

Vậy thể tích khối cầu $\large V = \dfrac{4}{3}\pi R^{3} = \dfrac{\sqrt{2}\pi a^{3}}{3}$ (đvtt).

Chọn A.