Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quan

Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng $\large 4\pi$. Diện tích mặt cầu $\large S_{mc}$ ngoại tiếp hình trụ là:

• A.

  A. $\large S_{mc} = 12\pi$

• B.

  B. $\large S_{mc} = 10\pi$

• C.

  C. $\large S_{mc} = 8\pi$

• D.

  D. $\large S_{mc} = 6\pi$

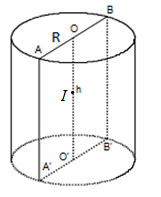
Do thiết diện qua trục là một hình vuông nên: OO' = AB = $\large 2R_{day}$ 

$\large \Rightarrow S_{xq} = 2\pi R_{day}h =  2\pi R_{day}.2R_{day} = 4\pi R_{day}^{2}$ 

$\large \Rightarrow R_{day} = \sqrt{\dfrac{S_{xq}}{4\pi }} = \sqrt{\dfrac{4\pi }{4\pi }} = 1$ .

Khối cầu ngoại tiếp hình trụ có tâm I là trung điểm của OO'. Do thiết diện qua trục là một hình vuông nên: O'I = O'A = $\large R_{day}$ = 1.

$\large R = IA = \sqrt{O'I^{2} + O'A^{2}} = \sqrt{1^{2} + 1^{2}} = \sqrt{2}$.

Suy ra diện tích mặt cầu: $\large S_{mc} = 4\pi R^{2} = 4\pi (\sqrt{2})^{2} = 8\pi$