Hình nón có đường cao 20 cm , bán kính đáy 25 cm . Một mặt phẳng ( P )

Hình nón có đường cao 20cm, bán kính đáy 25cm. Một mặt phẳng (P) qua đỉnh của hình nón và có khoảng cách đến tâm là 12cm. Diện tích thiết diện tạo bởi (P) và hình nón là:

• A.

  A. 450 $\large (cm^{2})$

• B.

  B. 500 $\large (cm^{2})$

• C.

  C. 600 $\large (cm^{2})$

• D.

  D. 550 $\large (cm^{2})$

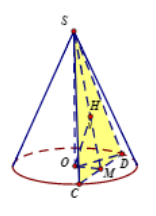
Theo đề:

h = 20, R = 25, OH = 12

Ta có:

$\large \dfrac{1}{OH^{2}} = \dfrac{1}{SO^{2}} + \dfrac{1}{OM^{2}}$ 

$\large \Leftrightarrow \dfrac{1}{OM^{2}} = \dfrac{1}{OH^{2}}-\dfrac{1}{SO^{2}}$ 
$\large \Leftrightarrow \dfrac{1}{OM^{2}} = \dfrac{1}{12^{2}}-\dfrac{1}{20^{2}} = \dfrac{1}{225}$ 

$\large \Rightarrow$ OM = 15 

$\large SM = \sqrt{SO^{2}+OM^{2}} = \sqrt{20^{2}+15^{2}} = 25$ 

$\large CD = 2CM = 2\sqrt{R^{2}-OM^{2}} = 2\sqrt{25^{2}-15^{2}} = 40$ 

Vậy $\large S_{\Delta SCD} = \dfrac{1}{2}SM.CD = \dfrac{1}{2}.40.25 = 500$.

Chọn đáp án B.