Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình ch
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi bằng 12. Giá trị lớn nhất của thể tích khối trụ là
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
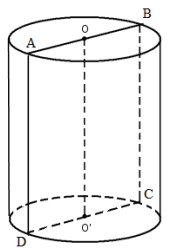
Từ hình vẽ ta có $\Large ABCD$ là hình chữ nhật, gọi chiều cao của hình trụ là $\Large h$ và bán kính đáy của hình trụ là $\Large r$, theo giả thiết ta có $\Large 2(h+2r)=12$ $\Large \Leftrightarrow h+2r=6$.
Thể tích của khối trụ tương ứng là $\Large V=\pi r^2h$, theo bất đẳng thức Cô si ta có
$\Large r+r+h\geq 3\sqrt[3]{r^2.h}$ $\Large \Leftrightarrow V=\pi r^2h\leq \pi .\left(\dfrac{2r+h}{3}\right)^3=8\pi$
Dấu bằng xảy ra khi và chỉ khi $\Large r=h=2$.
Vậy giá trị lớn nhất của thể tích khối trụ là $\Large 8\pi$.
Xem thêm các bài tiếp theo bên dưới
- Cho $\Large a, b, c$ là các số thực dương khác 1 thỏa mãn $\Large \mat
- Cho hàm số $\Large y=f(x)$. Hàm số $\Large y=f'(x)$ có đồ thị như hình
- Cho hình chóp $\Large S.ABC$ có đáy $\Large ABC$ là tam giác đều cạnh
- Số nghiệm của phương trình $\Large \mathrm{ln}(x^2-6x+7)=\mathrm{ln}(x
- Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình vuông tâm $