Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm $
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a. Biết SA vuông góc với mặt phẳng đáy và SA=a√3. Tính thể tích của khối chóp S.ABO.
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
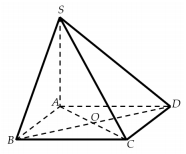
Do ABCD là hình vuông cạnh bằng 2a nên AC=BD=2a√2 ⇒OA=OB=2a√22=a√2
⇒SΔAOB=12OA.OB=12.a√2.a√2=a2 (đvdt).
Vậy thể tích của khối chóp S.ABO là VS.ABO=13SA.SΔABO=13.a√3.a2=a3√33 (đvdt).
Xem thêm các bài tiếp theo bên dưới
- Trong không gian Oxyz, cho ba điểm A(2;−1;3), $\La
- Một lớp có 15 học sinh nam và 20 học sinh nữ. Có bao nhiêu cách chọn 5
- Trong không gian với hệ tọa độ Oxyz, cho điểm $\Large I(2; -1
- Cho biết rằng bảng biến thiên sau là bảng biến thiên của một hàm số tr
- Trong không gian với hệ trục tọa độ Oxyz, tìm một véctơ chỉ p