Cho hình chóp $\Large S.ABC$ có đáy $\Large ABC$ là tam giác đều cạnh

Cho hình chóp $\Large S.ABC$ có đáy $\Large ABC$ là tam giác đều cạnh $\Large a$, $\Large SA$ vuông góc với mặt phẳng $\Large (ABC)$; góc giữa đường thẳng $\Large SB$ và mặt phẳng $\Large (ABC)$ bằng $\Large 60^{\circ}$. Gọi $\Large M$ là trung điểm cạnh $\Large AB$. Khoảng cách từ $\Large B$ đến $\Large (SMC)$ bằng

• A.

  $\Large \dfrac{a\sqrt{39}}{13}$.

• B.

  $\Large a\sqrt{3}$.

• C.

  $\Large a$.

• D.

  $\Large \dfrac{a}{2}$.

Chọn A

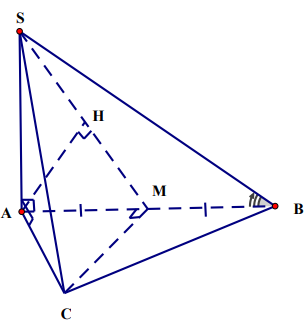
Ta có $\Large \widehat{\big(SB, (ABC)\big)}=\widehat{SBA}=60^{\circ}$ $\Large \Rightarrow SA=tan60^{\circ}.a=a\sqrt{3}$.

Vì $\Large M$ là trung điểm của $\Large AB$ $\Large \Rightarrow d\big(B, (SMC)\big)=d\big(A, (SMC)\big)$

Dựng $\Large AH$ vuông góc với $\Large SM$ tại $\Large H$ $\Large \Rightarrow d\big(A, (SMC)\big)=AH$ mà $\Large AM=\dfrac{1}{2}AB=\dfrac{a}{2}$.

Xét tam giác vuông $\Large \Delta SAM$ ta có: $\Large \dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AM^2}$ $\Large =\dfrac{1}{3a^2}+\dfrac{4}{a^2}=\dfrac{13}{3a^2}$ $\Large \Rightarrow AH=\dfrac{a\sqrt{39}}{13}$.