Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol (P
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol (P): y=x2y=x2 và đường thẳng d: y=2xy=2x quay quanh trục OxOx bằng
Đáp án án đúng là: A
Lời giải chi tiết:
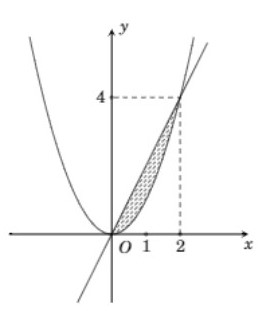
Xét phương trình x2=2x⇔x2−2x=0⇒[x=0x=2
Khi đó miền phẳng là phần gạch chéo hình bên. Gọi V là thể tích khối tròn xoay khi quay miền phẳng đó quanh trục Ox ta có V=π2∫0(2x)2dx−π2∫0(x2)2dx=π2∫04x2dx−π2∫0x4dx
Chọn đáp án A
Xem thêm các bài tiếp theo bên dưới
- Tích phân $\Large I=\int\limits_{0}^{1}{\dfrac{{{(x-1)}^{2}}}{{{x}^{2}
- Diện tích phần hình phẳng (phần tô màu) trong hình vẽ bên được tính th
- Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số $\La
- Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị (C) của
- Cho hình (H) là hình phẳng giới hạn bởi parabol $\Large y={{x