Gọi $\Large S$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $\La

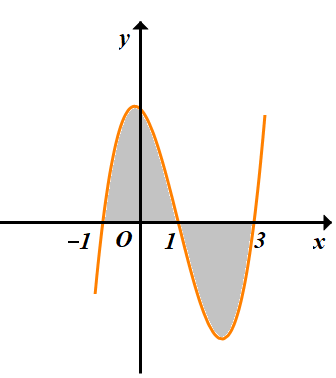
Gọi $\Large S$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $\Large f(x)=\dfrac{1}{3}{{x}^{3}}-{{x}^{2}}-\dfrac{1}{3}x+1$ và trục hoành như hình vẽ bên. Mệnh đề nào sau đây sai?

• A.

  $\Large S=\int\limits_{-1}^{1}{f(x)dx-\int\limits_{1}^{3}{f(x)dx}}$

• B.

  $\Large S=2\int\limits_{1}^{3}{f(x)dx}$

• C.

  $\Large S=2\int\limits_{-1}^{1}{f(x)dx}$

• D.

  $\Large S=\int\limits_{-1}^{3}{\left| f(x) \right|dx}$

Phương trình hoành độ giao điểm của đồ thị hàm số $\Large y=f(x)$ và trục hoành :

$\Large \dfrac{1}{3}{{x}^{3}}-{{x}^{2}}-\dfrac{1}{3}x+1=0$ $\Large \Leftrightarrow \left[ \begin{align}  & x=-1 \\  & x=1 \\  & x=3 \\ \end{align} \right.$

Từ hình vẽ ta thấy $\Large f(x)>0,\forall x\in \left( -1;1 \right)$ và $\Large f(x)<0,\forall x\in \left( 1;3 \right)$

Do đó diện tích $\Large S$ được tính bởi: 

$\Large S=\int\limits_{1}^{3}{\left| f(x) \right|dx=\int\limits_{3}^{1}{f(x)dx-\int\limits_{1}^{3}{f(x)dx=2\int\limits_{3}^{1}{f(x)dx}}}}$

vì $\Large \int\limits_{-1}^{1}{f(x)dx=\int\limits_{-1}^{1}{\left( \dfrac{1}{3}{{x}^{3}}-{{x}^{2}}-\dfrac{1}{3}x+1 \right)dx=\dfrac{4}{3}}}$ và $\Large \int\limits_{1}^{3}{f(x)dx=\int\limits_{1}^{3}{\left( \dfrac{1}{3}{{x}^{3}}-{{x}^{2}}-\dfrac{1}{3}x+1 \right)dx=-\dfrac{4}{3}}}$

Vậy mệnh đề sai là  $\Large S = 2\int\limits_{1}^{3}f(x)dx.$

Chọn đáp án B