Cho $\Large (H)$ là hình phẳng giới hạn bởi $\Large \dfrac{1}{4}$ cung

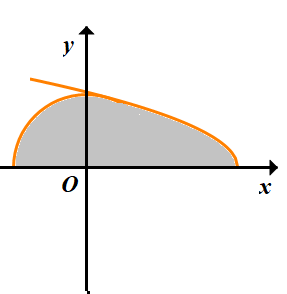
Cho $\Large (H)$ là hình phẳng giới hạn bởi $\Large \dfrac{1}{4}$ cung tròn có bán kính $\Large R=2$, đường cong $\Large y=\sqrt{4-x}$ và trục hoành ( miền tô đậm như hình vẽ ) . Tính thể tích $\Large V$ của khối tạo thành khi cho hình $\Large (H)$ quay quanh trục $\Large Ox$

• A.

  $\Large V=\dfrac{40\pi }{3}$

• B.

  $\Large V=\dfrac{66\pi }{7}$

• C.

  $\Large V=\dfrac{77\pi }{6}$

• D.

  $\Large V=\dfrac{8\pi }{3}$

Phương trình đường tròn tâm $\Large O$ có bán kính bằng 2 là $\Large {{x}^{2}}+{{y}^{2}}=4$ 

Vậy phương trình của nửa đường tròn trên trục hoành là $\Large y=\sqrt{4-x^2}$

Do đó: $\Large V=\pi \left[ \int\limits_{-2}^{0}{(4-{{x}^{2}})dx+\int\limits_{0}^{4}{(4-x)dx}} \right]=\dfrac{40}{3}\pi$

Chọn đáp án A