Ông An có một mảnh vườn hình elip có độ dài trục lớn $\Large 12m$ và đ

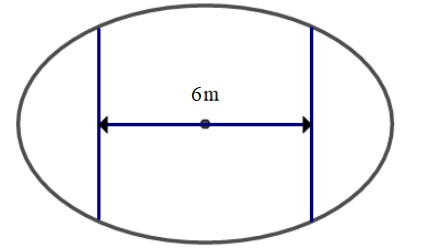
Ông An có một mảnh vườn hình elip có độ dài trục lớn $\Large 12m$ và độ dài trục bé $\Large 8m$. Ông muốn trồng hoa trên một mảnh đất rộng $\Large 6m$ và nhận trục bé của elip làm trục đối xứng như hình vẽ. Biết kinh phí trồng hoa là $\Large 90.000 \,đồng / m^2$. Hỏi ông An cần bao nhiêu tiền để trồng hoa trên mảnh đất đó (số tiền được làm tròn đến hàng nghìn)

• A.

  $\Large 6199000$

• B.

  $\Large 4133000$

• C.

  $\Large 4333000$

• D.

  $\Large 6198000$

Hướng dẫn:

Ta có độ dài trục lớn $\Large 2a=12\Rightarrow a=6$ và độ dài trục nhỏ $\Large 2b=8\Rightarrow b=4.$

Suy ra phương trình Elip: $\Large \dfrac{x^2}{36}+\dfrac{y^2}{16}=1$ $\Large \Rightarrow \left[\begin{array}{l} y=-\dfrac{4}{6}\sqrt{36-x^2}   \left(E_1\right) \\ y=\dfrac{4}{6}\sqrt{36-x^2}   \left(E_2\right) \end{array} \right.$

Khi đó diện tích dải vườn được giới hạn bởi các đường $\Large \left(E_1\right);$ $\Large \left(E_2\right);$ $\Large x=-3;$ $\Large x=3$

$\Large \Rightarrow S=2.\int_{-3}^{3}{\dfrac{4}{6}\sqrt{36-x^2}dx}$ $\Large =\dfrac{8}{3}.\int_{0}^{3}{\sqrt{36-x^2}dx}.$

Suy ra số tiền ông An cần là: $\Large T=S.90000$ $\Large =240000.\int_{0}^{3}{\sqrt{36-x^2}dx}$ $\Large \xrightarrow{Casio} \approx 4133000$ (đồng).

Đáp án B.