Từ một khúc gỗ hình trụ có đường kính $\Large 30cm$ , người ta cắt khú

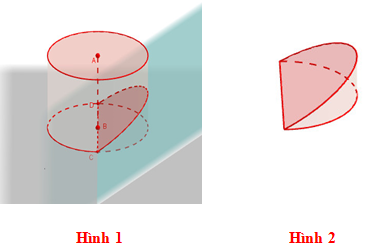
Từ một khúc gỗ hình trụ có đường kính $\Large 30cm$ , người ta cắt khúc gỗ bởi một mặt phẳng đi qua đường kính đáy và nghiêng với đáy một góc $\Large {{45}^{\circ }}$ để lấy một hình nêm ( xem hình minh họa dưới đây )

Kí hiệu $\Large V$ là thể tích của hình nêm ( hình 2 ). Tính $\Large V$.

• A.

  $\Large V=2250(c{{m}^{3}})$

• B.

  $\Large V=\dfrac{225\pi }{4}(c{{m}^{3}})$

• C.

  $\Large V=1250(c{{m}^{3}})$

• D.

  $\Large V=1350(c{{m}^{3}})$

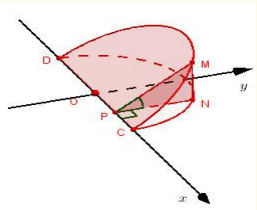
Chọn hệ trục tọa độ như hình vẽ. Khi đó hình nêm có đáy là nửa hình tròn có phương trình : $\Large y=\sqrt{225-{{x}^{2}}},x\in \left[ -15;15 \right]$

Một mặt phẳng cắt vuông góc với trục $\Large Ox$ tại điểm có hoành độ $\Large x$, $\Large \left( x\in \left[ -15;15 \right] \right)$

Cắt hình nêm theo thiết diện có diện tích là $\Large S(x)$ (xem hình )

Dễ thấy $\Large NP=y$ và $\Large MN=NP\tan {{45}^{\circ }}=y=\sqrt{15^2-{{x}^{2}}}$ khi đó $\Large S(x)=\dfrac{1}{2}MN.NP=\dfrac{1}{2}.(225-{{x}^{2}})$ suy ra thể tích hình nêm là: $\Large V=\int\limits_{-15}^{15}{S(x)dx=\int\limits_{-15}^{15}\dfrac{1}{2}.(225-{{x}^{2}})dx=2250(c{{m}^{3}})}$

Chọn A