Số nghiệm nguyên của bất phương trình $\Large (\sqrt{10}+3)^{\dfrac{3-

Số nghiệm nguyên của bất phương trình $\Large (\sqrt{10}+3)^{\dfrac{3-x}{x-1}}<(\sqrt{10}+3)^{\dfrac{x+1}{x+3}}$ trong khoảng $\Large (-2018; 2018)$ là:

• A.

  A. 4033

• B.

  B. 4032

• C.

  C. 4031

• D.

  D. 4030

Chọn D

ĐK: $\Large x\neq -3; x\neq 1$

BPT $\Large (\sqrt{10}+3)^{\dfrac{x-3}{x-1}}<(\sqrt{10}+3)^{\dfrac{x+1}{x+3}}$$\Large \Leftrightarrow \dfrac{x-3}{x-1}<\dfrac{x+1}{x+3}\Leftrightarrow \dfrac{-8}{(x-1)(x+3)}<0\Leftrightarrow (x-1)(x+3)>0$

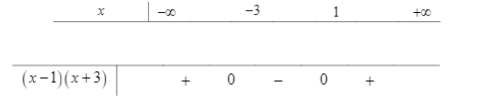
Vậy có số nghiệm nguyên trong khoảng (-2018; 2018) là 4030