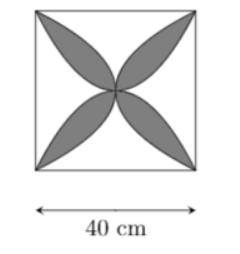
Một viên gạch hoa hình vuông cạnh 40 cm. Người ta đã dùng bốn đường pa

Một viên gạch hoa hình vuông cạnh 40 cm. Người ta đã dùng bốn đường parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn cánh hoa (phần tô đậm như hình vẽ). Diện tich của mỗi cánh hoa đó bằng

• A.

  $\Large 200\ cm^2$.

• B.

  $\Large \dfrac{800}{3}\ cm^2$.

• C.

  $\Large \dfrac{400}{3}\ cm^2$.

• D.

  $\Large \dfrac{200}{3}\ cm^2$.

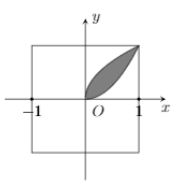
Đặt hình vuông vào hệ trục tọa độ $\Large Oxy$ như hình vẽ, cạnh của hình vuông ta có thể coi có độ dài bằng 1 trên hệ trục tọa độ.

Khi đó diện tích một cánh hoa chính là diện tích hình phẳng giới hạn bởi hai đồ thị $\Large y=x^2$ và $\Large y=\sqrt{x}$

Ta có

$\Large S_1=\int\limits_0^1(\sqrt{x}-x^2)dx=\dfrac{2}{3}x\sqrt{x}-\dfrac{x^3}{3}\bigg|_0^1=\dfrac{1}{3}$.

Vậy thực tế diện tích của mỗi cách hoa là

$\Large S=20\times 20\times S_1=\dfrac{400}{3}\ cm^2$.

Chọn phương án C