Cho hàm số $\Large f(x)$ có đạo hàm liên tục trên $\Large \mathbb{R}$

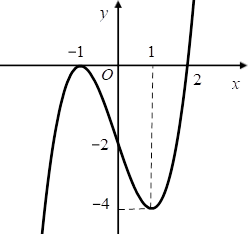
Cho hàm số $\Large f(x)$ có đạo hàm liên tục trên $\Large \mathbb{R}$ và có đồ thị hàm số $\Large y={f}'(x)$ như hình vẽ. Xét hàm số $\Large g(x)=f(x^2-2).$ Mệnh đề nào dưới đây sai?

• A.

  Hàm số g(x) nghịch biến trên (0; 2).

• B.

  Hàm số g(x) đồng biến trên $\Large (2; +\infty).$

• C.

  Hàm số g(x) nghịch biến trên (-1; 0).

• D.

  Hàm số g(x) nghịch biến trên $\Large (-\infty; -2).$

Ta có $\Large {g}'(x)={(x^2-2)}'.{f}'(x^2-2)=2x.{f}'(x^2-2).$

Hàm số nghịch biến khi $\Large {g}'(x) \leq 0 \Leftrightarrow x.{f}'(x^2-2) \leq 0$ $\Large \Leftrightarrow \left\{\begin{align} & x \leq 0 \\ & {f}'(x^2-2) \geq 0 \end{align}\right.$ hoặc $\Large \left\{\begin{align} & x \geq 0 \\ & {f}'(x^2-2) \leq 0 \end{align}\right.$

Từ đồ thị hình của hàm số $\Large y={f}'(x)$ như hình vẽ, ta thấy 

$\Large {f}'(x) \leq 0 \Leftrightarrow x \leq 2$ và $\Large {f}'(x) \geq 0 \Leftrightarrow x \geq 2.$

+ Với $\Large \left\{\begin{align} & x \leq 0 \\ & {f}'(x^2-2) \geq 0 \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & x \leq 0 \\ & x^2-2 \geq 2 \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & x \leq 0 \\ & x^2 \geq 4 \end{align}\right.$ $\Large \Leftrightarrow x\leq 0$ và $\Large \left[\begin{align} & x\geq 2 \\ & x\leq -2 \end{align}\right.$ $\Large \Leftrightarrow x \leq -2.$

+ Với $\Large \left\{\begin{align} & x \geq 0 \\ & {f}'(x^2-2) \leq 0 \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & x \geq 0 \\ & x^2-2 \leq 2 \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & x \geq 0 \\ & x^2 \leq 4 \end{align}\right.$ $\Large \Leftrightarrow 0 \leq x \leq 2.$

Như vậy hàm số nghịch biến trên mỗi khoảng $\Large (-\infty; -2), (0; 2);$ suy ra hàm số đồng biến trên $\Large (-2; 0)$ và $\Large (2; +\infty).$

Do $\Large (-1; 0) \subset (-2; 0)$ nên hàm số đồng biến trên $\Large (-1; 0).$ Vậy C sai.