Cho hai số phức $\Large z_1, z_2$ thỏa mãn $\Large |z_1+3-3i|=1$ và $\

Cho hai số phức $\Large z_1, z_2$ thỏa mãn $\Large |z_1+3-3i|=1$ và $\Large |z_2+1-2i|=|z_2-2+i|$. Giá trị nhỏ nhất của biểu thức $\Large P=|z_2+1-i|+|z_2-z_1|$ bằng:

• A.

  $\Large 4\sqrt{3}-1$.

• B.

  $\Large 4\sqrt{2}-1$.

• C.

  $\Large 2\sqrt{2}-1$.

• D.

  $\Large \sqrt{10}-1$.

Chọn B

Đặt: $\Large z_1=x_1+y_1i$ và $\Large z_2=x_2+y_2i$

$\Large |z_1+3-3i|=1$ $\Large \Leftrightarrow |x_1+3+(y_1-3)i|=1$ $\Large \Leftrightarrow (x_1+3)^2+(y_1-3)^2=1$

Suy ra tập hợp các điểm $\Large M(x_1; y_1)$ biểu diễn số phức $\Large z_1$ là đường tròn $\Large (C)$ tâm $\Large I(-3; 3)$ và bán kính $\Large r=1$.

$\Large |z_2+1-2i|=|z_2-2+i|$ $\Large \Leftrightarrow |x_2+1+(y_2-2)i|=|x_2-2+(y_2+1)i|$

$\Large \Leftrightarrow (x_2+1)^2+(y_2-2)^2=(x_2-2)^2+(y_2+1)^2$ $\Large \Leftrightarrow x_2-y_2=0$

Suy ra tập hợp các điểm $\Large N(x_2; y_2)$ biểu diễn số phức $\Large z_2$ là đường thẳng $\Large d: x-y=0$

Nhận xét: $\Large d(I, d)=\dfrac{|-6|}{\sqrt{2}}=3\sqrt{2} > 1=r\Rightarrow$ đường thẳng $\Large d$ nằm ngoài đường tròn $\Large (C)$.

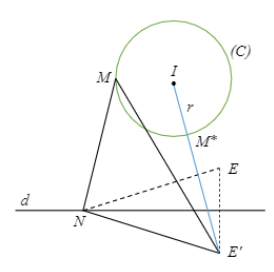
Gọi $\Large E(-1; 1)$. Ta thấy: $\Large E$ và $\Large M$ cùng phía so với đường thẳng $\Large d$.

Gọi $\Large {E}'(1; -1)$ đối xứng với $\Large E(-1; 1)$ qua đường thẳng $\Large d$. Khi đó:

$\Large P=|z_1+1-i|+|z_2-z_1|$ $\Large =EN+EM={E}'N+NM\geq {E}'M\geq {E}'M^*$ $\Large ={E}'I-r=4\sqrt{2}-1$.

Vậy: $\Large \min P=4\sqrt{2}-1$ đạt được khi: $\Large M\equiv M^*$