Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S)

MỤC LỤC
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S) tâm I(2;−1;−2) và đi qua gốc tọa độ O. Gọi d1,d2,d3 là ba đường thẳng thay đổi không đồng phẳng cùng đi qua O và cắt mặt cầu (S) tại điểm thứ hai là A,B,C. Khi thể tích của tứ diện OABC đạt giá trị lớn nhất thì mặt phẳng (ABC) đi qua điểm nào sau đây?
Đáp án án đúng là: D
Lời giải chi tiết:
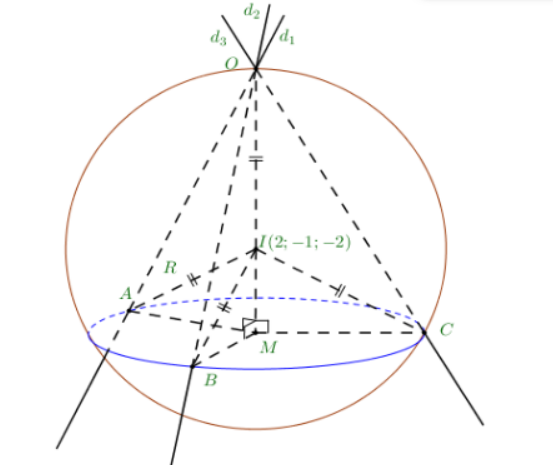
Chọn D
(S) tâm I(2;−1;−2) qua O ⇒R(S)=IA=IB=IC=IO=3=R
Đặt IM=x⇒AM=BM=CM=√R2−x2
⇒VOABC=13.OM.SΔABC≤13(R+x)(R2−x2)√34 (ΔABC đều)
Mà (R+x)(R2−x2)=(R+x)2(R−x)
=4(R+x2)(R+x2)(R−x)≤4(R+x2+R+x2+R−x)327=32R327
VOABCmax⇔R+x2=R−x ⇔3+x=6−2x⇒x=1⇒OM=4
⇒(ABC) qua M có →n(ABC)=→OM(OM⊥(ABC))
(OM):{x=2ty=−tz=−2t ⇒M(2t;−t;−2t) ⇒OM2=9t2=16 ⇒t=±43
⇒[M(83;−43;−83)M(−83;43;83) ⇒[(ABC):2x−y−2z−12=0(ABC):2x−y−2z+12=0
Thay E(−1;2;−8) vào phương trình mặt phẳng (ABC) ta thấy thỏa mãn phương trình. Suy ra khi thể tích của tứ diện OABC đạt giá trị lớn nhất thì mặt phẳng (ABC) đi qua điểm E(−1;2;−8).