Cho hình lăng trụ đứng $\Large ABC.A{}'B{}'C{}'$ có đáy là tam giác $\

Cho hình lăng trụ đứng $\Large ABC.A{}'B{}'C{}'$ có đáy là tam giác $\Large ABC$ vuông tại $\Large B$, $\Large AC = 2$, $\Large BC = 1$, $\Large AA{}' = 1$. Tính góc giữa đường thẳng $\Large AB{}'$ và $\Large (BCC{}'B{}')$

• A.

  $\Large 45^{o}$

• B.

  $\Large 30^{o}$

• C.

  $\Large 60^{o}$

• D.

  $\Large 90^{o}$

Chọn C

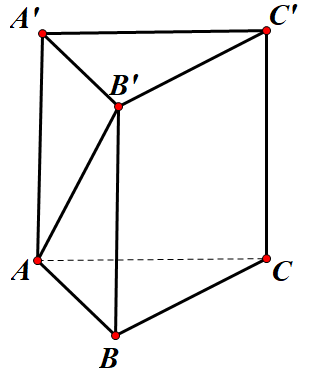
Do $\Large ABC.A{}'B{}'C{}'$ là lăng trụ đứng nên $\Large BB{}' \bot (ABC)$

=> $\Large BB{}' \bot AB$.

Mặt khác tam giác $\Large ABC$ vuông tại $\Large B$ nên $\Large AB \bot BC$.

Ta có:

$\Large \left\{\begin{array}{l}AB \bot BC \\BB{}' \bot AB\\\end{array}\right.$

$\Large \Rightarrow AB \bot (BCC{}'B{}')$ nên $\Large BB{}'$ là hình chiếu của $\Large AB{}'$ trên mặt phẳng $\Large (BCC{}'B{}')$.

Do đó: $\Large \left ( \widehat{AB{}', (BCC{}'B{}')} \right ) = \left ( \widehat{AB{}', B{}'B} \right ) = \widehat{AB{}'B}$

Trong tam giác $\Large AB{}'B$ vuông tại $\Large B$ ta có:

$\Large \tan \widehat {AB{}'B} = \dfrac{AB}{BB{}'} = \dfrac{\sqrt{AC^{2}-BC^{2}}}{BB{}'} = \dfrac{\sqrt{2^{2} - 1^{2}}}{1} = \sqrt{3}$

$\Large \Rightarrow \widehat{AB{}'B} = 60^{o}$

Vậy $\Large \left ( \widehat{AB{}', (BCC{}'B{}')} \right ) = \left ( \widehat{AB{}', B{}'B} \right ) = \widehat{AB{}'B} = 60^{o}$.