Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC); góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60∘. Gọi M là trung điểm cạnh AB. Khoảng cách từ B đến (SMC) bằng
Đáp án án đúng là: A
Lời giải chi tiết:
Chọn A
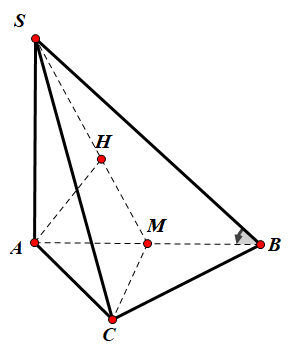
Ta có (SB,(ABC))=^SBA=60∘⇒SA=tan60∘.a=a√3.
Vì M là trung điểm của AB ⇒d(B,(SMC))=d(A,(SMC)).
Dựng AH vuông góc với SM tại H ⇒d(A,(SMC))=AH mà AM=12AB=a2.
Xét tam giác vuông ΔSAM ta có: 1AH2=1SA2+1AM2=13a2+4a2=133a2⇒AH=a√3913.
Xem thêm các bài tiếp theo bên dưới