Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều. Mặt phẳng (A

Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều. Mặt phẳng (A'BC) tạo với đáy góc $\Large 30^{\circ}$ và tam giác A'BC có diện tích bằng 8. Tính thể tích V của khối lăng trụ đã cho.

• A.

  $\Large 64\sqrt{3}.$

• B.

  $\Large 2\sqrt{3}.$

• C.

  $\Large 16\sqrt{3}.$

• D.

  $\Large 8\sqrt{3}.$

Chọn D

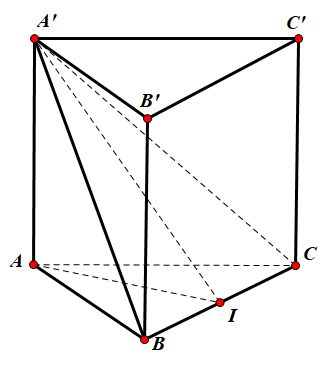
Gọi I là trung điểm cạnh BC.

Vì ABC.A'B'C' là lăng trụ đứng có đáy là tam giác đều nên ABC.A'B'C' là khối lăng trụ đều.

Do đó ta có: $\Large {A}'B={A}'C.$ Suy ra tam giác A'BC cân tại A' $\Large \Rightarrow {A}'I \perp BC.$

Mặt khác: tam giác ABC đều $\Large \Rightarrow AI \perp BC.$

Suy ra $\Large BC \perp ({A}'IA).$

Vậy góc giữa mặt phẳng (A'BC) và mặt đáy bằng góc $\Large \widehat{A'IA}=30^{\circ}.$

Ta có: tam giác ABC là hình chiếu của tam giác A'BC trên mặt đáy nên 

$\Large S_{ABC}=S_{{A}'BC}\cos \alpha=8.\cos 30^{\circ}=4\sqrt{3}.$

Đặt $\Large AB=x \Rightarrow S_{ABC}=\dfrac{x^2\sqrt{3}}{4}=4\sqrt{3} \Rightarrow x=4.$

Ta có: $\Large AI=\dfrac{x\sqrt{3}}{2}=2\sqrt{3} \Rightarrow A{A}'=AI.\tan \widehat{AI{A}'}=2.$

Suy ra: $\Large V_{ABC.{A}'{B}'{C}'}=A{A}'.S_{ABC}=2.4\sqrt{3}=8\sqrt{3}.$