Có bao nhiêu $\Large m$ nguyên để phương trình sau có đúng hai nghiệm

Có bao nhiêu $\Large m$ nguyên để phương trình sau có đúng hai nghiệm dương phân biệt $\Large (x^2-3x)2^{1+m+4x-x^2}=(x^2-4x-m)2^{2(x+m)}+x^2-2x+m$.

• A. 3.
• B. 4.
• C. 2.
• D. 1.

Phân tích ý tưởng:

Bài toán trên thuộc mức độ vận dụng cao. Để giải được bài toán trên cần có 3 mẫu chốt

Phân tích chuyển về bài toán dạng $\Large f(u)+f(v)=0$, với $\Large f(t)$ là một hàm số đơn điệu trên khoảng $\Large K$.
Khi đưa phương trình về dạng $\Large f(u)+f(v)=0$ thì cần chứng minh được $\Large f(u)$ và $\Large f(v)$ cùng dấu hoặc cùng bằng 0.
Sử dụng phương pháp đồ thị để giải quyết vấn đề của bài.
Đặt $\Large \left\{\begin{align} & u=x^2-4x-m\\ & v=x^2-2x+m\end{align}\right.$, phương trình đã cho trở thành

$\Large (u+v)2^{-u}=u2^{v-u}+v$ $\Large \Leftrightarrow (u+v)\dfrac{1}{2^u}=u2^{v-u}+v$

$\Large \Leftrightarrow u+v=u2^v+v2^u$

$\Large \Leftrightarrow u(1-2^v)=v(2^u-1)$ (*)

1. Nếu $\Large u=0$ thì phương trình (*) luôn đúng.

2. Nếu $\Large v=0$ thì phương trình (*) luôn đúng.

3. Nếu $\Large u.v\neq 0$ thì phương trình (*) $\Large \Leftrightarrow \dfrac{2^u-1}{u}=\dfrac{1-2^v}{v}$ $\Large \Leftrightarrow \dfrac{2^u-1}{u}+\dfrac{2^v-1}{v}=0$.

Xét hàm số $\Large f(t)=\dfrac{2^t-1}{t}$, $\Large t\neq 0$. Ta có

Nếu $\Large t > 0\Rightarrow 2^t > 1\Rightarrow 2t-1 > 0\Rightarrow f(t) > 0, \forall t > 0$.
Nếu $\Large t < 0\Rightarrow 2^t < 1\Rightarrow 2^t-1 < 0\Rightarrow f(t) > 0, \forall t < 0$.
Từ đó suy ra $\Large f(t)=\dfrac{2^t-1}{t} > 0, \forall t\neq 0$.

Mà phương trình (1) $\Large \Leftrightarrow f(u)+f(v)=0$ (vô lý) vì $\Large \left\{\begin{align} & f(u) > 0\\ & f(v) > 0\end{align}\right.$, $\Large \forall u, v\neq 0$.

Do đó, phương trình đã cho tương đương với $\Large \left[\begin{align} & u=0\\ & v=0\end{align}\right.$ $\Large \Rightarrow \left[\begin{align} & x^2-4x-m=0\\ & x^2-2x+m=0\end{align}\right.$ $\Large \Leftrightarrow \left[\begin{align} & x^2-4x=m\ (2)\\ & -x^2+2x=m\ (3)\end{align}\right.$

Xét hai hàm số $\Large y=x^2-4x$ và $\Large y=-x^2+2x$ với $\Large x > 0$. Ta có đồ thị như hình vẽ.

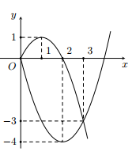
Dựa vào đồ thị, ta thấy phương trình đã cho có đúng hai nghiệm dương phân biệt khi $\Large m\in \begin{Bmatrix} -4; -3; 0; 1 \end{Bmatrix}$.

Vậy có 4 giá trị nguyên của tham số $\Large m$.

Chọn đáp án B