Cho hình lăng trụ đứng ABC.A'B'C' có $\Large A{A}'=AB=AC=1$ và $\Large

Cho hình lăng trụ đứng ABC.A'B'C' có $\Large A{A}'=AB=AC=1$ và $\Large \widehat{BAC}=120^{\circ}.$ Gọi I là trung điểm cạnh CC'. Côsin góc giữa hai mặt phẳng (ABC) và (AB'I) bằng

• A.

  $\Large \dfrac{\sqrt{370}}{20}.$

• B.

  $\Large \dfrac{\sqrt{70}}{10}.$

• C.

  $\Large \dfrac{\sqrt{30}}{20}.$

• D.

  $\Large \dfrac{\sqrt{30}}{10}.$

Chọn D

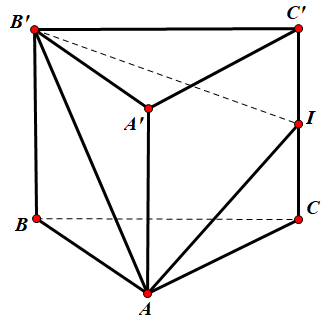
Gọi $\Large \varphi$ là góc giữa hai mặt phẳng (ABC) và (AB'I).

$\Large A{B}'=\sqrt{2}, AI=\dfrac{\sqrt{5}}{2}.$

$\Large BC^2=AB^2+AC^2-2AB.AC.{\rm{cos}}\,A=3 \Rightarrow BC={B}'{C}'=\sqrt{3}.$

$\Large {B}'I=\sqrt{{B}'{C}'^2+{C}'I^2}=\dfrac{\sqrt{13}}{2}.$

Vì $\Large A{B}'^2+AI^2={B}'I^2 \Rightarrow \Delta A{B}'I$ vuông tại A.

$\Large S_{ABC}=\dfrac{1}{2}AB.AC.sinA=\dfrac{\sqrt{3}}{4}$ và $\Large S_{A{B}'I}=\dfrac{1}{2}AI.A{B}'=\dfrac{\sqrt{10}}{4}.$

Hình chiếu vuông góc của $\Large \Delta A{B}'I$ lên mặt phẳng (ABC) là $\Large \Delta ABC.$

Ta có $\Large S_{ABC}=S_{A{B}'I}.\cos\varphi \Rightarrow \cos\varphi=\dfrac{S_{ABC}}{S_{A{B}'I}}=\dfrac{\sqrt{30}}{10}.$