Một mạch điện gồm 4 linh kiện như hình vẽ, trong đó xác suất hỏng của

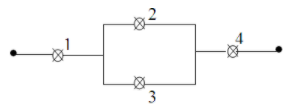
Một mạch điện gồm 4 linh kiện như hình vẽ, trong đó xác suất hỏng của từng linh kiện trong một khoảng thời gian t nào đó tương ứng là 0,2; 0,1; 0,05 và 0,02. Biết rằng các linh kiện làm việc độc lập với nhau và các dây dẫn điện luôn tốt. Tính xác suất để mạng điện hoạt động tốt trong khoảng thời gian t.

• A. 0,78068
• B. 0,78008
• C. 0,7808
• D. 0,78808

Mạng điện hoạt động tốt khi một trong các trường hợp sau xảy ra:

+ Trường hợp 1: Linh kiện 1, 2, 4 hoạt động tốt, linh kiện 3 bị hỏng

Xác suất là: $\Large P_{1}=(1-0,2) \cdot(1-0,1) \cdot 0,05 \cdot(1-0,02)$

+ Trường hợp 2; Linh kiện 1, 3, 4 hoạt động tốt, linh kiện 2 bị hỏng

Xác xuất là: $\Large P_{2}=(1-0,2) \cdot 0,1 \cdot(1-0,05) \cdot(1-0,02)$

+ Trường hợp 3: Tất cả linh kiện 1, 2, 3, 4 đều hoạt động tốt

Xác xuất là: $\Large P_{3}=(1-0,2) \cdot(1-0,1) \cdot(1-0,05) \cdot(1-0,02)$

Vậy xác suất để mạng điện hoạt động tốt trong khoảng thời gian t là: $\Large P=P_{1}+P_{2}+P_{3}=0,78008$