Một mạch dao động LC lí tưởng gồm cuộn cảm thuần L và tụ điện C có hai

Một mạch dao động LC lí tưởng gồm cuộn cảm thuần L và tụ điện C có hai nhân bản A và B. Trong mạch đang có dao động điện từ tự do với chu kì T, biên độ điện tích của tụ điện bằng $Q_o$. Tại thời điểm t, điện tích bản A là ${{q}_{A}}=\frac{{{Q}_{o}}}{2}$ và đang tăng. Sau khoảng thời gian $\Delta t$  nhỏ nhất thì điện tích của bản B là ${{q}_{B}}={{Q}_{o}}$. Giá trị của $\Delta t$ là

• A. T/6
• B. 2T/3
• C. 5T/12
• D. T/3

Phương pháp: sử dụng công thức tính thời gian bằng đường tròn.

Cách giải: ta có phương trình điện tích: $q={{Q}_{o}}\cos \left( \omega t+\varphi  \right)$ ban đầu A được tích điện 1/2 $Q_o$ và đang tăng nên pha ban đầu có giá trị $\varphi =-\frac{\pi }{3}$. Khi bản B có điện tích cực dại $Q_o$ thì bản A có điện tích -$Q_o$. ta có vecto quay như hình vẽ:

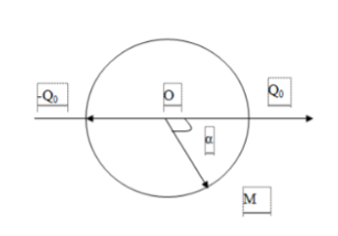
Ta có:

$\cos \alpha =\frac{{{Q}_{o}}/2}{{{Q}_{o}}}=\frac{1}{2}\Rightarrow \alpha ={{60}^{o}}$

$\Rightarrow \beta ={{180}^{o}}+{{60}^{o}}={{240}^{o}}$

$\Rightarrow \Delta t=\frac{240}{360}T=\frac{2}{3}T$