Một mạch dao động LC lí tưởng gồm cuộn dây thuần cảm có L=2mH và tụ đi

Một mạch dao động LC lí tưởng gồm cuộn dây thuần cảm có L=2mH và tụ điện có điện dung C=2nF. Khi năng lượng điện trường bằng một nửa năng lượng từ trường cực đại thì dòng điện trong mạch có độ lớn $\sqrt{2}$A; Lấy gốc thời gian là lúc dòng điện trong mạch có giá trị bằng một nửa giá trị cực đại và tụ đang phóng điện. Biểu thức cường độ dòng điện trong mạch là

• A. $i=2\cos \left( {{5.10}^{5}}t-\frac{\pi }{3} \right)A$
• B. $i=2\cos \left( {{5.10}^{5}}t-\frac{2\pi }{3} \right)A$
• C. $i=2\cos \left( {{5.10}^{5}}t+\frac{2\pi }{3} \right)A$
• D. $i=2\cos \left( {{5.10}^{5}}t+\frac{\pi }{3} \right)A$

Phương pháp: viết phương trình cường độ dòng điện trong mạch

Cách giải: giải sử phương trình điện tích là: $q={{Q}_{o}}\cos \left( \omega t+\varphi  \right)$

Phương trình cường độ dòng điện là: i=q’=$-\omega {{Q}_{o}}\sin \left( \omega t+\varphi  \right)={{I}_{o}}\cos \left( \omega t+\varphi +\frac{\pi }{2} \right)$

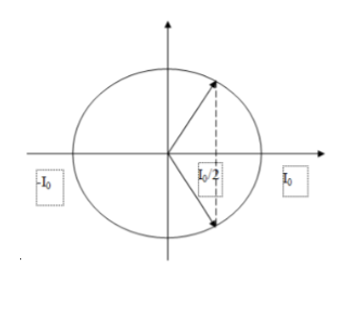
Tụ đang phóng điện tức là q đang giảm, ta có hình vẽ:

Vì q đang giảm nên I đang tăng và ta có phương trình của I là: $i={{I}_{o}}\cos \left( \omega t-\frac{\pi }{3} \right)$

Với tần số góc : $\omega =\frac{1}{\sqrt{LC}}={{5.10}^{5}}rads$

Khi năng lượng điện trường bằng một nửa năng lượng từ trường cực đại thì năng lượng từ trường cũng bằng một nửa năng lượng từ trường cực đại nên: $\frac{1}{2}L{{i}^{2}}=\frac{1}{2}\frac{1}{2}L{{I}_{o}}^{2}$

$\Rightarrow {{I}_{o}}^{2}=2{{i}^{2}}=2{{\sqrt{2}}^{2}}=4\Rightarrow {{I}_{o}}=2A$

Vậy phương trình của dòng điện I là: $i=2\cos \left( {{5.10}^{5}}t-\frac{\pi }{3} \right)A$