Một khối nón có bán kính đáy bằng 2 cm , chiều cao bằng $\large \sqrt{

MỤC LỤC
Câu hỏi:
Một khối nón có bán kính đáy bằng 2 cm, chiều cao bằng $\large \sqrt{3}$ cm. Một mặt phẳng đi qua đỉnh và tạo với đáy một góc $\large 60^{\circ}$ chia khối nón làm 2 phần. Tính thể tích V phần nhỏ hơn (Tính gần đúng đến hàng phần trăm).
Đáp án án đúng là: A
Lời giải chi tiết:
Chọn A
Cách 1:
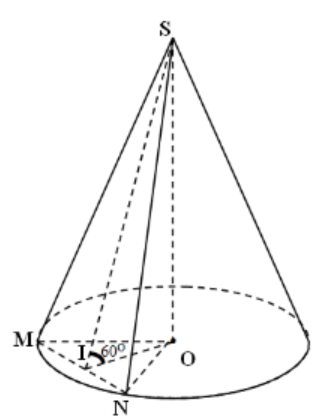
Gọi mặt phẳng đi qua đỉnh và tạo với đáy một góc $\large 60^{\circ}$ cắt khối nón theo thiết diện là tam giác SMN như hình vẽ.
Gọi I là trung điểm MN. Khi đó $\large OI \perp MN$ và $\large SI \perp MN$, suy ra góc giữa mặt phẳng (SMN) và mặt đáy là góc $\large \widehat{SIO} = 60^{\circ}$.
Xét tam giác SIO ta có: $\large OI = \dfrac{SO}{tan\widehat{SIO}} = \dfrac{\sqrt{3}}{tan60^{\circ}} = 1$.
$\large IN = \sqrt{ON^{2}-OI^{2}} = \sqrt{3}$, $\large MN = 2.IN = 2\sqrt{3}$.
$\large S_{\Delta OMN} = \dfrac{1}{2}.OI.MN = \sqrt{3}$.
$\large V_{S.OMN} = \dfrac{1}{3}.SO.S_{\Delta OMN} = 1$.
$\large V_{k/non} = \dfrac{1}{3}.\pi .2^{2}.\sqrt{3} = \dfrac{4\sqrt{3}}{3}\pi$.
$\large sin\widehat{ION} = \dfrac{IN}{ON} = \dfrac{\sqrt{3}}{2}$
Suy ra $\large \widehat{ION} = 60^{\circ}, \widehat{MON} = 2.\widehat{ION} = 120^{\circ}$.
Gọi V là thể tích cần tính
Ta có $\large V = \dfrac{1}{3}V_{k/non}-V_{S.OMN} = \dfrac{4\sqrt{3}}{9}\pi - 1 \approx 1,42$ $\large cm^{3}$.
Cách 2:
Gọi mặt phẳng đi qua đỉnh và tạo với đáy một góc $\large 60^{\circ}$ cắt khối nón theo thiết diện là tam giác SMN như hình vẽ.
Gọi I là trung điểm MN. Khi đó $\large OI \perp MN$ và $\large SI \perp MN$, suy ra góc giữa mặt phẳng (SMN) và mặt đáy là góc $\large \widehat{SIO} = 60^{\circ}$.
Xét tam giác SIO ta có: $\large OI = \dfrac{SO}{tan\widehat{SIO}} = \dfrac{\sqrt{3}}{tan60^{\circ}} = 1$.
$\large IN = \sqrt{ON^{2}-OI^{2}} = \sqrt{3} \Rightarrow MN = 2.IN = 2\sqrt{3}$.
$\large S_{\Delta OMN} = \dfrac{1}{2}.OI.MN = \sqrt{3}$.
Ta có $\large sin\widehat{ION} = \dfrac{IN}{ON} = \dfrac{\sqrt{3}}{2}$ suy ra $\large \widehat{ION} = 60^{\circ}, \widehat{MON} = 2.\widehat{ION} = 120^{\circ}$.
Gọi $\large S_{V}$ là diện tích hình viên phân tạo bởi dây MN và cung nhỏ MN.
Ta có $\large S_{V} = \dfrac{1}{3}\pi R^{2}-S_{\Delta OMN} = \dfrac{4\pi }{3}-\sqrt{3}$
Thể tích phần nhỏ cần tính là: $\large V = \dfrac{1}{3}.SO.S_{V} = \dfrac{4\sqrt{3}}{9}\pi -1 \approx 1,42$ $\large cm^{3}$.
Xem thêm các bài tiếp theo bên dưới
- Cho hình thang ABCD có $\large \widehat{A} = \widehat{B} = 90^{\circ}$
- Cho khối trụ ( T ), AB và CD lần lượt là hai đường kính trên các mặt đ
- Cho hình trụ có bán kính đáy R và chiều cao R , lấy hai điểm A, B nằm
- Cho hình trụ có đáy là hai đường tròn tâm O và O’ , bán kính đáy bằng
- Cho hình vuông BCD cạnh a . Gọi N là điểm thuộc cạnh AD sao cho AN = 2