Cho hình vuông BCD cạnh a . Gọi N là điểm thuộc cạnh AD sao cho AN = 2
Lưu về Facebook:
MỤC LỤC
Câu hỏi:
Cho hình vuông BCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho AN = 2ND. Đường thẳng qua N vuông góc với BN cắt BC tại K. Tính thể tích V của khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK là:

Đáp án án đúng là: A
Lời giải chi tiết:
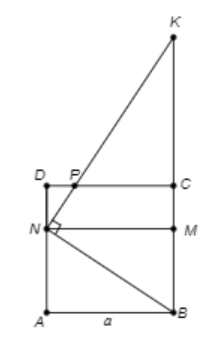
Ta có $\large NB = \sqrt{a^{2}+\dfrac{4a^{2}}{9}} = \dfrac{a\sqrt{13}}{3}$
$\large \Delta ABN$ đồng dạng $\large \Delta NKB$ suy ra:
$\large \dfrac{AN}{NB} = \dfrac{NB}{KB} \Rightarrow KB = \dfrac{NB^{2}}{AN} = \dfrac{13a^{2}}{9}.\dfrac{3}{2a} = \dfrac{13a}{6}$
Gọi M là điểm trên BC sao cho BM = 2MC
Suy ra $\large BM = \dfrac{2a}{3}; MK = \dfrac{3a}{2}$
Vậy $\large V = \pi a^{2}.\dfrac{2a}{3}+\dfrac{1}{3}\pi a^{2}.\dfrac{3a}{2} = \dfrac{7}{6}\pi a^{3}$
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Đường thẳng SA
- Hình lập phương có bao nhiêu trục đối xứng? A. 7 B. 9 C. 11 D. 13 Đườn
- Hình lập phương có tất cả bao nhiêu mặt phẳng đối xứng? A. 8 B. 9 C. 1
- Trong các mệnh đề sau, mệnh đề nào đúng? A. Tồn tại một hình đa diện c
- Số đỉnh của hình bát diện đều là bằng bao nhiêu? A. 10 B. 8 C. 6 D. 12