Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Đường thẳng SA

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với đáy (ABCD). Gọi H là hình chiếu của A trên đường thẳng SB. Bán kính mặt cầu ngoại tiếp tứ diện HBCD có giá trị nào sau đây?

• A.

  A. $\large a\sqrt{2}$

• B.

  B. a

• C.

  C. $\large \dfrac{a\sqrt{2}}{2}$

• D.

  D. $\large \dfrac{a}{2}$

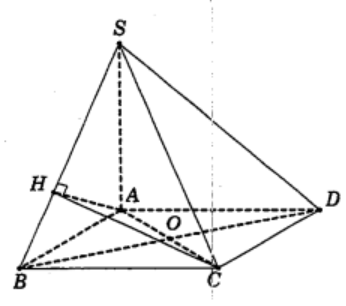
Gọi $\large O = AC \cap BD$.

Vì ABCD là hình vuông nên OB = OD = OC.  (1)

Ta có $\large \left\{\begin{matrix} CB \perp AB & \\  CB \perp SA &  \end{matrix}\right.\Rightarrow CB \perp (SAB)\Rightarrow CB \perp AH$ 

Lại có $\large AH \perp SB$ 

Suy ra $\large AH \perp (SBC) \Rightarrow AH \perp HC$ nên tam giác AHC vuông tại H và có O là trung điểm cạnh huyền AC nên suy ra OH = OC.   (2)

Từ (1) và (2), suy ra

 R = OH = OB = OD = OC = $\large \dfrac{a\sqrt{2}}{2}$. Chọn C.