Cho hình trụ có đáy là hai đường tròn tâm O và O’ , bán kính đáy bằng
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D; trên đường tròn tâm O’ lấy điểm B, C sao cho AB // CD và AB không cắt OO’. Tính AD để thể tích khối chóp O’.ABCD đạt giá trị lớn nhất.
Đáp án án đúng là: A
Lời giải chi tiết:
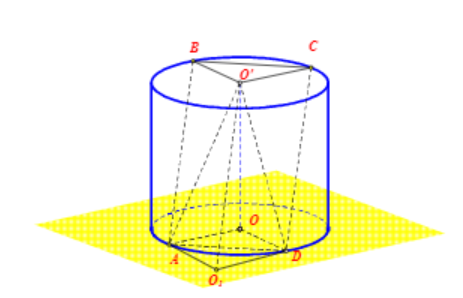
Kẻ đường thẳng qua O’ song song với AB cắt mặt phẳng chứa đường tròn (O) tại O1O1.
Lúc đó AO1D.BO′C là một hình lăng trụ chiều cao bằng 2a.
Vì AD = BC nên SΔBO′C=SΔOAD
Ta có thể tích của khối chóp O’.ABCD:
VO′.ABCD=13VAO1D.BO′C=23.2a.SBO′C=23.2a.SOAD
=23.2a.12.2a.2a.sin^AOD≤8a33
(VO′.ABCD)max⇔^AOD=90∘⇔AD=2√2a.
Xem thêm các bài tiếp theo bên dưới
- Cho hình vuông BCD cạnh a . Gọi N là điểm thuộc cạnh AD sao cho AN = 2
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Đường thẳng SA
- Hình lập phương có bao nhiêu trục đối xứng? A. 7 B. 9 C. 11 D. 13 Đườn
- Hình lập phương có tất cả bao nhiêu mặt phẳng đối xứng? A. 8 B. 9 C. 1
- Trong các mệnh đề sau, mệnh đề nào đúng? A. Tồn tại một hình đa diện c