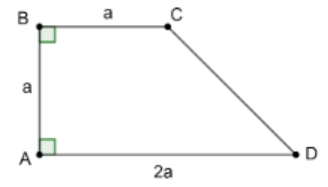
Cho hình thang ABCD có $\large \widehat{A} = \widehat{B} = 90^{\circ}$
MỤC LỤC
Câu hỏi:
Cho hình thang ABCD có $\large \widehat{A} = \widehat{B} = 90^{\circ}$, AB = BC = a, AD = 2a. Tính thể tích khối tròn xoay sinh ra khi quay hình thang ABCD xung quanh trục CD.

Đáp án án đúng là: A
Lời giải chi tiết:
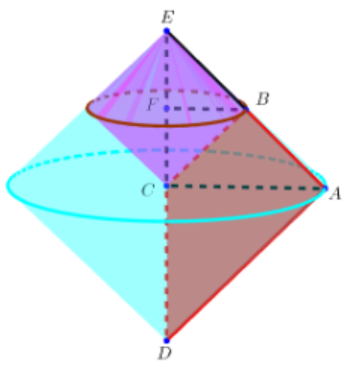
Gọi E là giao điểm của AB và CD. Gọi F là hình chiếu vuông góc của B trên CE.
Ta có: $\large \Delta BCF = \Delta BEF$ nên tam giác $\large \Delta BCF$ và $\large \Delta BEF$ quay quanh trục CD tạo thành hai khối nón bằng nhau có thể tích $\large V_{1}$.
$\large \Delta ADC = \Delta AEC$ nên tam giác $\large \Delta ADC$ và $\large \Delta AEC$ quay quanh trục CD tạo thành hai khối nón bằng nhau có thể tích V.
Nên thể tích khối tròn xoay sinh ra khi quay hình thang ABCD xung quanh trục CD bằng:
$\large 2V-2V_{1} = 2.\dfrac{1}{3}\pi (CD.AC^{2}-CF.BF^{2}) = \dfrac{2}{3}\pi \left [(a\sqrt{2})^{3}-\left (\dfrac{a}{\sqrt{2}} \right )^{3} \right ] = \dfrac{7\sqrt{2}\pi a^{3}}{6}$ (đvtt).
Xem thêm các bài tiếp theo bên dưới
- Cho khối trụ ( T ), AB và CD lần lượt là hai đường kính trên các mặt đ
- Cho hình trụ có bán kính đáy R và chiều cao R , lấy hai điểm A, B nằm
- Cho hình trụ có đáy là hai đường tròn tâm O và O’ , bán kính đáy bằng
- Cho hình vuông BCD cạnh a . Gọi N là điểm thuộc cạnh AD sao cho AN = 2
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Đường thẳng SA