Cho khối trụ ( T ), AB và CD lần lượt là hai đường kính trên các mặt đ
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho khối trụ (T), AB và CD lần lượt là hai đường kính trên các mặt đáy của khối (T). Biết góc giữa AB và CD là 30∘, AB = 6cm và thể tích khối ABCD là 30cm3. Khi đó thể tích khối trụ (T) là:
Đáp án án đúng là: A
Lời giải chi tiết:
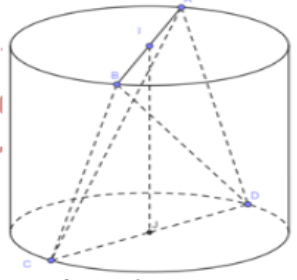
Chọn A.
Gọi h, V lần lượt là chiều cao và thể tích khối trụ (T).
⇒ d(AB,CD) = h (cm).
Ta có:
VABCD=16h.sin(AB;CD).AB.CD=16h.sin30∘.62⇒h=6VABCDsin30∘.62=10 (cm).
⇒VT=π(AB2)2.h=90π(cm3)
Xem thêm các bài tiếp theo bên dưới
- Cho hình trụ có bán kính đáy R và chiều cao R , lấy hai điểm A, B nằm
- Cho hình trụ có đáy là hai đường tròn tâm O và O’ , bán kính đáy bằng
- Cho hình vuông BCD cạnh a . Gọi N là điểm thuộc cạnh AD sao cho AN = 2
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Đường thẳng SA
- Hình lập phương có bao nhiêu trục đối xứng? A. 7 B. 9 C. 11 D. 13 Đườn