Cho hình trụ có bán kính đáy R và chiều cao R , lấy hai điểm A, B nằm
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình trụ có bán kính đáy R và chiều cao R, lấy hai điểm A, B nằm trên hai đường tròn đáy sao cho AB = 2R. Tính khoảng cách từ AB đến trục hình trụ theo R.
Đáp án án đúng là: A
Lời giải chi tiết:
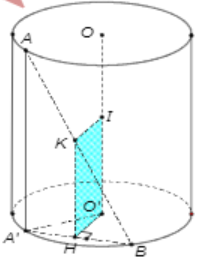
Giả sử A ∈ đường tròn O, B ∈O′. Từ A vẽ đường song song OO’ cắt đường tròn (O’) tại A’.
Vẽ O’H vuông góc A’B.
Từ H vẽ đường thẳng song song với OO’, cắt AB tại K. Vẽ KI // O’H.
Ta có: O′H⊥A′B và AA’ nên: O′H⊥mp(AA′B)⇒O′H⊥HK và AB.
Vậy tứ giác KIO’H là hình chữ nhật ⇒KI⊥OO′.
Vậy KI là đoạn vuông góc chung của AB và OO’. ΔAA′B vuông
⇒A′B2=AB2−AA′2=4R2−R2=3R2
Do H trung điểm A’B nên:
HA′=R√32.ΔO′A′H⇒O′H2=O′A2−A′H2=R2−3R24=R24.
Do đó: d(AB,OO’) = KI = O’H = R2.
Chọn A
Xem thêm các bài tiếp theo bên dưới
- Cho hình trụ có đáy là hai đường tròn tâm O và O’ , bán kính đáy bằng
- Cho hình vuông BCD cạnh a . Gọi N là điểm thuộc cạnh AD sao cho AN = 2
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Đường thẳng SA
- Hình lập phương có bao nhiêu trục đối xứng? A. 7 B. 9 C. 11 D. 13 Đườn
- Hình lập phương có tất cả bao nhiêu mặt phẳng đối xứng? A. 8 B. 9 C. 1