Một họa tiết hình cánh bướm như hình vẽ bên. Phần tô đậm đươ

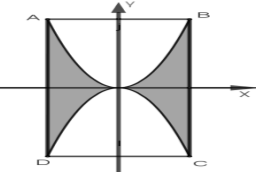
Một họa tiết hình cánh bướm như hình vẽ bên.

Phần tô đậm được đính đá với giá thành

 $\Large 500.000\text{/}{{\text{m}}^{\text{2}}}$. Phần còn lại được tô màu với giá thành  $\Large 250.000/{{m}^{2}}$.Cho $\Large AB=4dm;BC=8dm.$Hỏi để trang trí  $\Large 1000$ họa tiết như vậy cần số tiền gần nhất với số nào sau đây.

• A. $\Large 105660667$.
• B. $\Large 106666667$.
• C. $\Large 107665667$.
• D. $\Large 108665667$.

Vì $\Large AB=4dm;BC=8dm.$$\Large \Rightarrow A(-2;4),$$B(2;4),C(2;-4),D(-2;-4)$.
parabol là: $\Large y={{x}^{2}}$ hoặc $\Large y=-{{x}^{2}}$
Diện tích phần tô đậm là  $\Large {{S}_{1}}=4\int\limits_{0}^{2}{{{x}^{2}}dx=\dfrac{32}{3}\begin{matrix}
{}  \\
\end{matrix}(d{{m}^{2}})}$
Diện tích hình chữ nhật là  $\Large S=4.8=32\begin{matrix}
{}  \\
\end{matrix}({{m}^{2}})$
Diện tích phần trắng là  $\Large {{S}_{2}}=S-{{S}_{1}}=32-\dfrac{32}{3}=\dfrac{64}{3}\begin{matrix}
{}  \\
\end{matrix}(d{{m}^{2}})$
Tổng chi phí trang chí là:  $\Large T=\left( \dfrac{32}{3}.5000+\dfrac{64}{3}.2500 \right).1000\approx 106666667$