Cho số phức z thỏa mãn $\Large \left| z+\overline{z} \right|+\left| z-

Cho số phức z thỏa mãn $\Large \left| z+\overline{z} \right|+\left| z-\overline{z} \right|=4$. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $\Large P=\left| z-2-2i \right|$. Đặt $\Large A=M+m$. Mệnh đề nào sau đây là đúng?

• A. $\Large A\in \left( \sqrt{34};6 \right)$.
• B. $\Large A\in \left( 6;\sqrt{42} \right)$.
• C. $\Large A\in \left( 2\sqrt{7};\sqrt{33} \right)$.
• D. $\Large A\in \left( 4;3\sqrt{3} \right)$.

Giả sử: $\Large z=x+yi,\left( x,y\in \mathbb{R} \right)\Rightarrow N\left( x;y \right)$: điểm biểu diễn của số phức z trên mặt phẳng tọa độ  .
Ta có:
$\Large \left| z+\overline{z} \right|+\left| z-\overline{z} \right|=4\Leftrightarrow \left| x \right|+\left| y \right|=2\,\Rightarrow N$ thuộc các cạnh của hình vuông BCDF (hình vẽ).

 
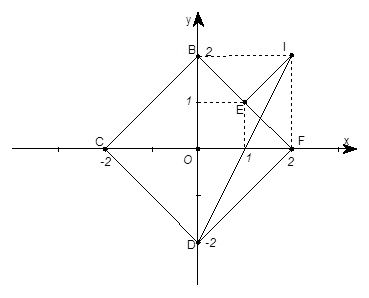
$\Large P=\left| z-2-2i \right|\Rightarrow P=\sqrt{{{\left( x-2 \right)}^{2}}+{{\left( y-2 \right)}^{2}}}\Rightarrow P=d\left( I;N \right)$ với $\Large I\left( 2;\,2 \right)$
Từ hình ta có: $\Large E\left( 1;\,1 \right)$
$\Large M={{P}_{\text{max}}}=ID=\sqrt{{{4}^{2}}+{{2}^{2}}}=2\sqrt{5}$ và $\Large m={{P}_{\text{min}}}=IE=\sqrt{{{\left( 2-1 \right)}^{2}}+{{\left( 2-1 \right)}^{2}}}=\sqrt{2}$
Vậy, $\Large A=M+m=2+2\sqrt{5}\in \left( \sqrt{34};6 \right)$