Một hình trụ có bán kính đáy bằng chiều cao và bằng $\Large a.$ Một hì

Một hình trụ có bán kính đáy bằng chiều cao và bằng $\Large a.$ Một hình vuông $\Large ABCD$ có $\Large AB, CD$ là hai dây cung của hai đường tròn đáy và mặt phẳng $\Large (ABCD)$ không vuông góc với đáy. Diện tích hình vuông đó bằng.

• A.

  A. $\Large \dfrac{5a^2}{4}.$

• B.

  B. $\Large \dfrac{5a^2\sqrt{2}}{4}.$

• C.

  C. $\Large 5a^2.$

• D.

  D. $\Large \dfrac{5a^2}{2}.$

Chọn D

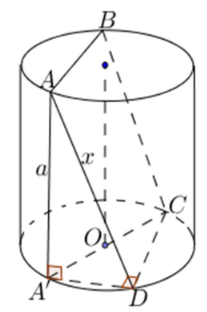
Kẻ đường sinh $\Large A'A.$

Khi đó ta có $\Large \left\{\begin{align} & CD \perp AD \\ & CD \perp {A}'A \end{align}\right.$ $\Large \Rightarrow CD \perp ({A}'AD)$ $\Large \Rightarrow CD \perp {A}'D$ $\Large \Rightarrow \widehat{{A}'DC}=90^{\circ}.$

Ta có $\Large \widehat{{A}'DC}$ là góc nội tiếp chắn nửa đường tròn $\Large \Rightarrow {A}'C=2a.$

Đặt cạnh hình vuông $\Large ABCD$ là $\Large x.$

Ta có $\Large \left\{\begin{align} & {A}'D^2=AD^2-{A}'A^2=x^2-a^2 \\ & {A}'D^2+DC^2={A}'C^2 \Rightarrow A'D^2+x^2=4a^2 \end{align}\right.$ $\Large \Rightarrow 2x^2-a^2=4a^2 \Rightarrow x^2=S_{ABCD}=\dfrac{5a^2}{2}.$