Cho hàm số y=f(x). Đồ thị hàm số y=f′(x) như hình
Lưu về Facebook:
MỤC LỤC
Câu hỏi:
Cho hàm số y=f(x). Đồ thị hàm số y=f′(x) như hình vẽ. Cho bất phương trình 3f(x)≥x3−3x+m (m là tham số thực). Điều kiện cần và đủ để bất phương trình 3f(x)≥x3−3x+m đúng với mọi x∈[−√3;√3] là
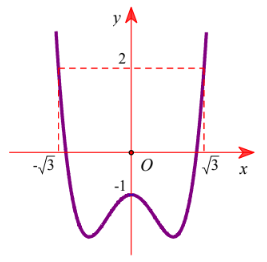
Đáp án án đúng là: D
Lời giải chi tiết:
Chọn D
Ta có 3f(x)≥x3−3x+m ⇔3f(x)−x3+3x≥m
Đặt g(x)=3f(x)−x3+3x. Tính g′(x)=3f′(x)−3x2+3
Có g′(x)=0⇔f′(x)=x2−1
Nghiệm của phương trình g′(x)=0 là hoành độ giao điểm của đồ thị hàm số y=f′(x) và parabol y=x2−1
Dựa vào đồ thị hàm số ta có: f′(x)=x2−1 ⇔[x=−√3x=0x=√3
BBT
Để bất phương trình nghiệm đúng với mọi x∈[−√3;√3] thì m≤min[−√3;√3]g(x)=g(√3)=3f(√3).