Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=a√3
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=a√3 và AD=a. Góc giữa hai đường thẳng B′D′ và AC bằng
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
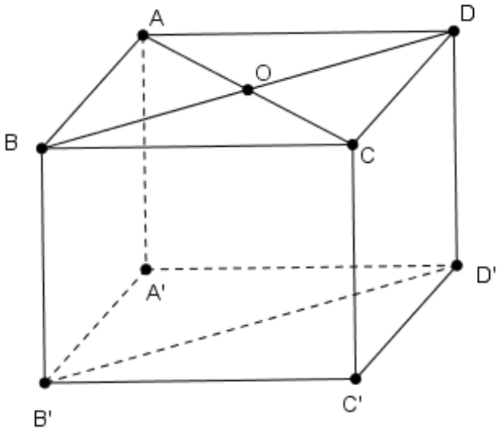
Ta có ^(B′D′;AC)=^(BD;AC).
Xét tam giác AOB có OA=OB=12AC=12√AB2+BC2=a nên:
cos^AOB=OA2+OB2−AB22OA.OB=−12;
⇒^AOB=120∘⇒^(B′D′;AC)=60∘.
Xem thêm các bài tiếp theo bên dưới