Cho hình hộp ABCD.A′B′C′D′ có các cạnh bằng 2a. Biết
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình hộp ABCD.A′B′C′D′ có các cạnh bằng 2a. Biết ^BAD=60∘, ^A′AB=^A′AD=120∘. Tính thể tích V của khối hộp ABCD.A′B′C′D′.
Đáp án án đúng là: A
Lời giải chi tiết:
Chọn A
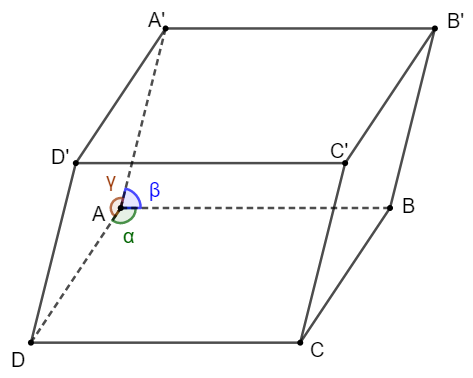
Ta có: VA.A′BD=16.AA′.AB.AD.√1−cos2α−cos2β−cos2γ+2.cosαcosβcosγ
⇒VA.A′BD=2√23a3
Mà VA.A′BD=16.VABCD.A′B′C′D′ ⇒VABCD.A′B′C′D′=4√2a3.