Một hình nón có bán kính $\Large R=4$. Một mặt phẳng qua đỉnh của hình

Một hình nón có bán kính $\Large R=4$. Một mặt phẳng qua đỉnh của hình nón cắt hình nón theo thiết diện có diện tích $\Large S=4\sqrt{6}$ và cắt đường tròn đáy theo dây cung có độ dài bằng 4. Chiều cao của hình nón bằng

• A.

  2.

• B.

  $\Large 3\sqrt{2}$.

• C.

  $\Large 2\sqrt{3}$.

• D.

  4.

Chọn C

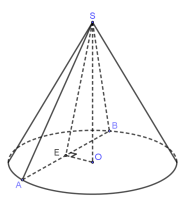
Giả sử hình nón đỉnh $\Large S$, gọi $\Large O$ là tâm đường tròn đáy. Thiết diện qua đỉnh là tam giác cân $\Large SAB$ có diện tích bằng $\Large 4\sqrt{6}$. Gọi $\Large E$ là trung điểm dây cung $\Large AB$. Ta có $\Large OE\perp AB$.

Có $\Large S_{\Delta SAB}=\dfrac{1}{2}.SE.AB\Rightarrow SE=\dfrac{2S_{\Delta SAB}}{AB}=\dfrac{2.4\sqrt{6}}{4}=2\sqrt{6}$.

Trong tam giác vuông $\Large OEB$, có $\Large OE^2=OB^2-EB^2=16-4=12$.

Trong tam giác vuông $\Large SOE$, có $\Large SO^2=SE^2-EO^2=24-12=12\Rightarrow SO=2\sqrt{3}$. Vậy hình nón có chiều cao bằng $\Large 2\sqrt{3}$.