Tập tất cả các giá trị của tham số $\Large m$ để phương trình $\Large

Tập tất cả các giá trị của tham số $\Large m$ để phương trình $\Large 4^{\cos x}-2^{\cos x+1}+2m-1=0$ có đúng 3 nghiệm $\Large x\in \left[-\dfrac{\pi}{2}; \pi \right]$ là

• A.

  $\Large (1; 2)$.

• B.

  $\Large \left[\dfrac{7}{8}; 1\right)$.

• C.

  $\Large \left(-1; \dfrac{7}{8}\right)$.

• D.

  $\Large (0; 1)$.

Chọn B

Ta có $\Large 4^{\cos x}-2^{\cos x+1}+2m-1=0$ $\Large \Leftrightarrow (2^{\cosx})^2-2.2^{\cosx}+2m-1=0$.

Đặt $\Large t=2^{\cosx}$ vì $\Large x\in \left[-\dfrac{\pi}{2}; \pi \right]$ nên $\Large t\in \left[\dfrac{1}{2}; 2\right]$.

Ta được phương trình $\Large t^2-2t+2m-1=0\Leftrightarrow 2m=-t^2+2t+1$. (1)

Nhận xét:

+) Với $\Large \dfrac{1}{2}\leq t < 1$ hoặc $\Large t=2$ có 1 nghiệm $\Large x\in \left[-\dfrac{\pi}{2}; \pi \right]$.

+) Với $\Large 1\leq t < 2$ có đúng 2 nghiệm $\Large x\in \left[-\dfrac{\pi}{2}; \pi \right]$.

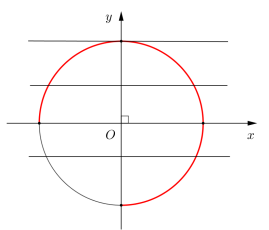
Hình minh họa quan hệ giữa giá trị của $\Large t$ và số nghiệm $\Large x$ 

Xét hàm số $\Large f(t)=-t^2+2t+1$ với $\Large t\in \left[\dfrac{1}{2}; 2\right]$, có $\Large f'(t)=-2t+2\Rightarrow f'(t)=0\Leftrightarrow t=1$.

Bảng biến thiên:

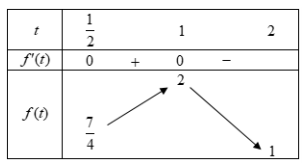
Suy ra phương trình $\Large 4^{\cos x}-2^{cos x+1}+2m-1=0$ có đúng 3 nghiệm $\Large x\in \left[-\dfrac{\pi}{2}; \pi \right]$ khi và chỉ khi phương trình (1) có 2 nghiệm $\Large \dfrac{1}{2}\leq t_1 < 1 \leq t_2 < 2$.

Từ bảng biến thiên suy ra $\Large \dfrac{7}{4}\leq 2m < 2\Leftrightarrow \dfrac{7}{8}\leq m < 1$.

Vậy $\Large m\in \left[\dfrac{7}{8}; 1\right)$.