Cho hình hộp $\Large ABCD.A'B'C'D'$ có đáy $\Large ABCD$ là hình thoi

Cho hình hộp $\Large ABCD.A'B'C'D'$ có đáy $\Large ABCD$ là hình thoi cạnh $\Large a$, $\Large \widehat{ABC}=60^{\circ}$, $\Large AA'=2a$, hình chiếu vuông góc của điểm $\Large A$ trên mặt phẳng $\Large (A'B'C'D')$ là trọng tâm tam giác $\Large A'B'C'$. Gọi $\Large M$ là một điểm di động trên cạnh $\Large BB'$. Khoảng cách từ điểm $\Large M$ đến mặt phẳng $\Large (CDD'C')$ là

• A.

  $\Large \dfrac{\sqrt{165}a}{30}$.

• B.

  $\Large \dfrac{2\sqrt{165}a}{15}$.

• C.

  $\Large \dfrac{\sqrt{165}a}{15}$.

• D.

  $\Large \dfrac{\sqrt{165}a}{5}$.

Chọn C

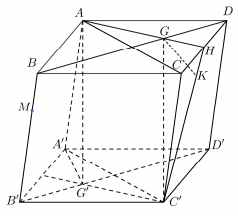
Gọi $\Large G$ và $\Large G'$ lần lượt là trọng tâm các tam giác $\Large ADC$ và $\Large A'B'C'$.

Từ giả thiết suy ra: $\Large AG'\perp (A'B'C'D')$ và $\Large C'G\perp (ABCD)$.

Do đáy $\Large ABCD$ là hình thoi cạnh $\Large a$ và $\Large \widehat{ABC}=60^{\circ}$ nên các tam giác $\Large A'B'C'$ và $\Large ADC$ là các tam giác đều.

Ta có $\Large (ABB'A')|| (CDD'C')$

$\Large \Rightarrow d\big(M, (CDD'C')\big)=d\big(A, (CDD'C')\big)=3d\big(G, (CDD'C')\big)$

Tam giác $\Large ADC$ đều nên $\Large AG\perp CD$ tại trung điểm $\Large H$ của $\Large CD$.

Có $\Large C'G\perp (ABCD)\Rightarrow C'G\perp CD$.

Do đó, $\Large CD\perp (GHC')\Rightarrow (GHC')\perp (CDD'C')$.

Từ $\Large G$ dựng $\Large GK\perp C'H\Rightarrow GK\perp (CDD'C')\Rightarrow GK=d\big(G, (CDD'C')\big)$.

Có $\Large C'G=AG'=\sqrt{AA'^2-A'G'^2}=\sqrt{4a^2-\left(\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}\right)^2}=\dfrac{a\sqrt{11}}{\sqrt{3}}$.

Xét tam giác $\Large GHC'$ có $\Large C'G=\dfrac{a\sqrt{11}}{\sqrt{3}}$; $\Large GH=\dfrac{a\sqrt{3}}{6}$.

$\Large \dfrac{1}{GK^2}=\dfrac{1}{C'G^2}+\dfrac{1}{GH^2}$=$\Large \dfrac{3}{11a^2}+\dfrac{12}{a^2}=\dfrac{135}{11a^2}$ $\Large \Rightarrow GK=\dfrac{a\sqrt{165}}{45}$.

Vậy $\Large d\big(M, (CDD'C')\big)=3d\big(G, (CDD'C')\big)=3GK=\dfrac{a\sqrt{165}}{15}$.