Cho hai số thực $\Large x, y$ thỏa mãn $\Large \mathrm{log}_2(2x+4y-1)

Cho hai số thực $\Large x, y$ thỏa mãn $\Large \mathrm{log}_2(2x+4y-1)\geq \mathrm{log}_{\sqrt{2}}\sqrt{x^2+y^2}$ với $\Large x\leq 0$. Gọi M, N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $\Large P=y-x$. Giá trị của M+N bằng:

• A.

  $\Large 3+2\sqrt{2}-\sqrt{3}$.

• B.

  $\Large 4+2\sqrt{2}-\sqrt{3}$.

• C.

  $\Large 5+\sqrt{3}-\sqrt{2}$.

• D.

  4.

Chọn A

Điều kiện xác định: $\Large 2x+4y-1 > 0$, $\Large x, y$ không đồng thời bằng 0.

Với điều kiện xác định như trên ta được:

$\Large \mathrm{log}_2(2x+4y-1)\geq \mathrm{log}_{\sqrt{2}}\sqrt{x^2+y^2}$

$\Large \Leftrightarrow \mathrm{log}_2(2x+4y-1)\geq \mathrm{log}_2(x^2+y^2)$

$\Large \Leftrightarrow2x+4y-1\geq x^2+y^2$

$\Large \Leftrightarrow(x^2-2x+1)+(y^2-4y+4)\leq 4$

$\Large \Leftrightarrow(x-1)^2+(y-2)^2\leq 4$

Như vậy, các điểm $\Large (x; y)$ thỏa mãn bất phương trình nằm trên đường tròn và trong hình tròn tâm $\Large I(1; 2)$ bán kính $\Large R=2$.

Mặt khác, vì $\Large x\leq 0$ nên tập hợp các điểm $\Large (x; y)$ là phần hình tròn nằm trên trái trục tung như hình.

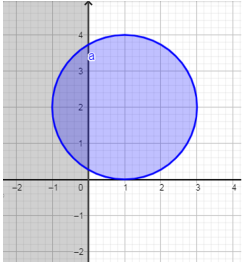
Tại $\Large x=0$ ta có:

$\Large (0-1)^2+(y-2)^2\leq 4\Leftrightarrow (y-2)^2\leq 3$ $\Large \Leftrightarrow -\sqrt{3}\leq y-2\leq \sqrt{3}$ $\Large \Leftrightarrow 2-\sqrt{3}\leq y \leq 2+\sqrt{3}$

Như vậy, $\Large P=y-x\geq y\geq 2-\sqrt{3}$ ($\Large x\leq 0$; $\Large y\geq 2-\sqrt{3}$)

Dấu bằng xảy ra khi $\Large x=0$, $\Large y=2-\sqrt{3}$.

Mặt khác, áp dụng bất đẳng thức Bu-nhi-a cốp-xki ta được:

$\Large P=y-x=(y-2)+(1-x)+1\leq \sqrt{\big(1^2+1^2\big)\big[(y-2)^2+(1-x)^2\big]}+1=1+2\sqrt{2}$

Dấu bằng xảy ra khi

$\Large \left\{\begin{align} & \dfrac{y-2}{1}=\dfrac{1-x}{1} \\ & y-x=1+2\sqrt{2} \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & x=1-\sqrt{2} \\ & y=2+\sqrt{2} \end{align}\right.$ (thỏa mãn điều kiện $\Large x\leq 0$; $\Large 2-\sqrt{3}\leq y \leq 2+\sqrt{3}$)

Như vậy, $\Large M=1+2\sqrt{2}$, $\Large N=2-\sqrt{3}$.

Suy ra: $\Large M+N=3+2\sqrt{2}-\sqrt{3}$.