Một hình nón bị cắt bởi mặt phẳng $\large (P)$ song song với đáy. Mặt

Một hình nón bị cắt bởi mặt phẳng $\large (P)$ song song với đáy. Mặt phẳng $\large (P)$ chia hình nón làm hai phần $\large (N_{1})$ và $\large (N_{2})$. Cho hình cầu nội tiếp $\large (N_{2})$ như hình vẽ sao cho thể tích hình cầu bằng một nửa thể tích của $\large (N_{2})$ . Một mặt phẳng đi qua trục hình nón và vuông góc với đáy cắt $\large (N_{2})$ theo thiết diện là hình thang cân, tang góc nhọn của hình thang cân là

• A.

  $\large 1$

• B.

  $\large 2$

• C.

  $\large 4$

• D.

  $\large \sqrt {3}$

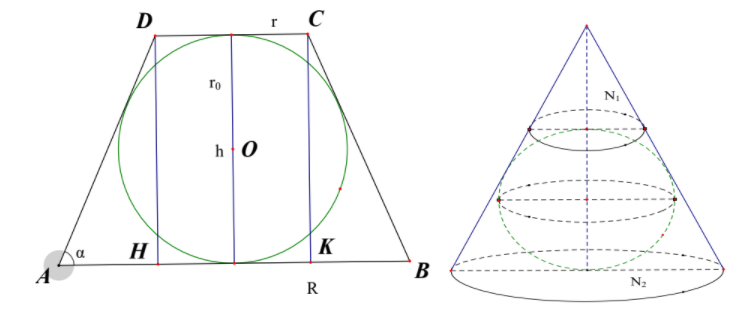
Giả sử ta có mặt cắt của hình nón cụt và các đại lượng như hình vẽ.
Gọi $\large \alpha$  là góc cần tìm. Xét $\large \Delta AHD$ vuông tại H có $\large DH = h , AH = R - r \Rightarrow h = 2r_{0} = AH .tan \alpha = (R - r) tan \alpha $  (1)
Thể tích khối cầu $\large V_{1} = \dfrac {4}{3} \pi r_{0}^{3} = \dfrac {\pi h^{3}}{6}$
Thể tích của  $\large (N_{2})$ là $\large V_{2} = \dfrac {1}{3} \pi h (R^{2} + r^{2} + Rr)$
$\large \dfrac {1}{2} = \dfrac {V_{1}}{V_{2}} \Rightarrow h^{2} = R^{2} + r^{2} + Rr$   (2)
Ta có: $\large BC = R + r$  (tính chất hai tiếp tuyến cắt nhau)
Mà $\large h^{2} = BC^{2} - (R - r)^{2}  = 4Rr$   (3) 
Từ (2), (3) $\large \Rightarrow (R - r)^{2}  = Rr$  (4)
Từ (1), (3), (4) $\large \Rightarrow h^{2} = (R - r)^{2} . tan^{2} \alpha = 4(R - r)^{2}$   (vì $\large \alpha$ là góc nhọn)
$\large \Rightarrow tan^{2} \alpha = 4 \Rightarrow  tan \alpha = 2$.