Cho hàm số bậc bốn $\large y = f(x)$ có đồ thị hàm số $\large y = f'(x

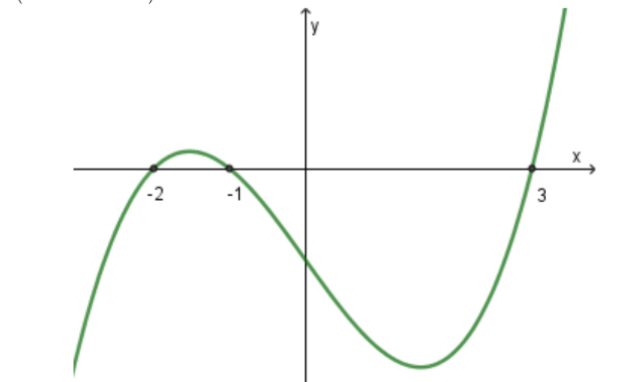
Cho hàm số bậc bốn $\large y = f(x)$ có đồ thị hàm số $\large y = f'(x)$ như hình bên dưới. Gọi $\large S$ là tập hợp tất cả các giá trị nguyên của tham số $\large m$ thuộc [1;2020] để hàm số $\large g(x) = f(x^{4} - 2x^{2} + m)$ có đúng 3 điểm cực trị. Tổng tất cả các phần tử của $\large S$ là 

• A.

  2041200

• B.

  2041204

• C.

  2041195

• D.

  2041207

Ta có: $\large g'(x) = (4x^{3} - 4x) f'(x^{4} - 2x^{2} + m)$

$\large g'(x) = 0 \Leftrightarrow$ $\large \left[\begin{align} &4x^{3} - 4x = 0 (1) \\ &f'(x^{4} - 2x^{2} + m) = 0 (2) \end{align}\right.$
(1) $\large \Leftrightarrow \left[\begin{align} x = 1  \\ x = 0 \\ x = -1 \end{align}\right.$
(2) $\large \Leftrightarrow \left[\begin{align} x^{4} - 2x^{2} + m = -2  \\ x^{4} - 2x^{2} + m = -1 \\ x^{4} - 2x^{2} + m = 3 \end{align}\right.$ $\large \Leftrightarrow  \left[\begin{align} -m = x^{4} - 2x^{2} + 2 = g_{1}( x)  \\ -m = x^{4} - 2x^{2} + 1 = g_{2} (x) \\ -m = x^{4} - 2x^{2} - 3 = g_{3} (x) \end{align}\right.$
Ta có bảng biến thiên của các hàm số $\large g_{1} (x),  g_{2} (x),  g_{3} (x)$ như hình vẽ

 

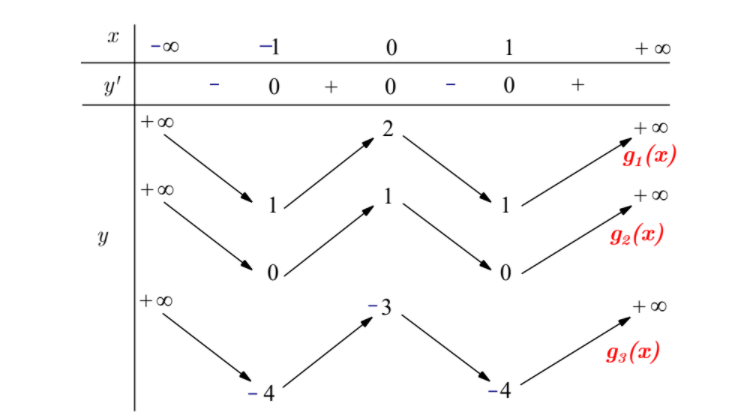
Từ bảng biến trên, ta dễ thấy: với $\large -m \leq -4 \Leftrightarrow m \geq 4$ hàm số $\large g(x) = f(x^{4} - 2x^{2} + m)$ 3 điểm cực trị.

Do đó: S = {4;5; 6; 7;...; 2020} 
Vậy tổng tất cả các phần tử của S là: $\large 4 + 5 + 6 + ... + 2020 = \dfrac {(4 + 2020)2017}{2} = 2041024$