Cho hình chóp S.ABCD có đáy ABCD là hình bình hành v

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích là V. Điểm P là trung điểm của SC. Mặt phẳng (α) qua AP cắt hai cạnh SB và SD lần lượt tại M và N. Gọi V1 là thể tích của khối chóp S.AMPN. Tìm giá trị nhỏ nhất của tỷ số V1V
Đáp án án đúng là: C
Lời giải chi tiết:
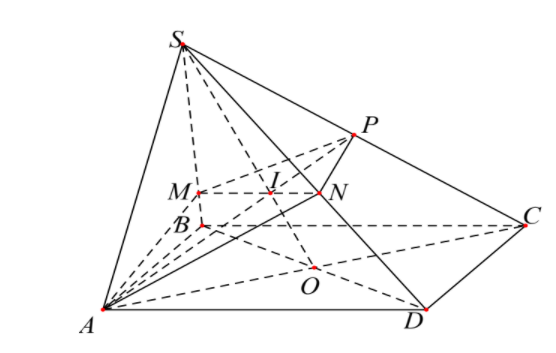
Đặt a=SMSB;b=SNSD (0<a;b≤1)
Ta có: V1V=VS.AMP+VS.ANPV=VS.AMP2VS.ABC+VS.ANP2VS.ADC=12(SMSB.SPSC+SNSD.SPSC)=14(a+b) (1)
Lại có: V1V=VS.AMN+VS.PMNV=VS.AMN2VS.ABD+VS.PMN2VS.CBD=12(SMSB.SNSD+SMSB.SPSC.SNSD)=34ab (2)
Suy ra: 14(a+b)=34ab⇔a+b=3ab⇒b=a3a−1. Từ điều kiện, ta có: a3a−1≤1 hay a≥12
Thay vào (2) ta được tỉ số V1V=34.a23a−1
Đặt f(a)=34.a23a−1;a∈[12;1], ta có: f′(a)=34.3a2−2a(3a−1)2=0⇔ [a=0(L)a=23
f(12)=f(1)=38;f(23)=13
Do đó: MinV1V=Mina∈[12;1]f(a)=f(23)=13
Cách 2:
Từ giả thiết và cách dựng thiết diện ta có: SASA=a=1;SBSM=b;SCSP=c=2;SDSN=d⇒a+c=b+d=3
Khi đó: V1V=a+b+c+d4.a.b.c.d=64.1.2.b.d=34b.d≥34(b+d2)2=13⇒V1V≥13
⇒ MinV1V=13
Xem thêm các bài tiếp theo bên dưới