Một đoạn mạch gồm điện trở có giá trị R, cuộn cảm thuần có độ tự cảm L

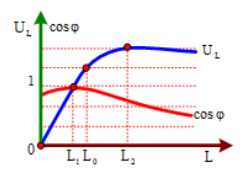
Một đoạn mạch gồm điện trở có giá trị R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp theo thứ tự đó, các giá trị R và C cố định, cuộn dây thuần có độ tự cảm L thay đổi được. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của điện áp hai đầu cuộn cảm UL và hệ số công suất $\Large cos\alpha $ của đoạn mạch theo giá trị của hệ số tự cảm L. Tại thời điểm $\Large\ L = L_0$, hệ số công suất hai đầu mạch chứa phần tử R, L là? 

• A.

  A. 0,96

• B.

  B. 0,69

• C.

  C. 0,75

• D.

  D. 0,82

+ $\Large\ L={{L}_{1}}\Rightarrow \cos \varphi =1\Rightarrow {{Z}_{L!}}={{Z}_{C}}$ 
+ $\Large\ L={{L}_{2}}\Rightarrow {{U}_{L\max }}\Rightarrow {{Z}_{L2}}=\dfrac{{{R}^{2}}+Z_{C}^{2}}{{{Z}_{C}}}=\dfrac{{{R}^{2}}+Z_{L1}^{2}}{{{Z}_{L!}}}\left( 1 \right)$ 
+ Dựa vào đồ thị ta thấy: $\Large\ {{U}_{L!}}=\dfrac{3}{5}{{U}_{L2}}\Leftrightarrow \dfrac{U}{R}{{Z}_{L!}}=\dfrac{3}{5}\dfrac{U}{R}\sqrt{{{R}^{2}}+Z_{L2}^{2}}\Rightarrow {{Z}_{L1}}=\dfrac{3}{4}R\left( 2 \right)$ 
+ Mặt khác: $\Large\ \left\{ \begin{align}
  & L={{L}_{0}} \\ 
 & L=\pm \infty  \\ 
\end{align} \right.\Rightarrow {{U}_{L0}}={{U}_{L\infty }}\Rightarrow \frac{1}{{{L}_{0}}}+\dfrac{1}{+\infty }=\dfrac{2}{{{L}_{2}}}\Rightarrow {{Z}_{L2}}=2{{Z}_{L0}}\left( 3 \right)$ 
+ Thế (2); (3) vào (1) ta được: $\Large\ 2{{Z}_{L0}}=\dfrac{{{R}^{2}}+{{\left( \dfrac{3}{4}R \right)}^{2}}}{\dfrac{3}{4}R}\Rightarrow {{Z}_{L0}}=\dfrac{25}{25}R$ 
+ Vậy khi $\Large\ L={{L}_{0}}\Rightarrow \cos {{\varphi }_{RC}}=\dfrac{R}{\sqrt{{{R}^{2}}+Z_{L0}^{2}}}=\dfrac{1}{\sqrt{1+{{\left( \dfrac{25}{24} \right)}^{2}}}}=0,69$ 

→ Đáp án A