Cho mạch điện xoay chiều như hình vẽ, trong đó giá trị biến trở R và đ

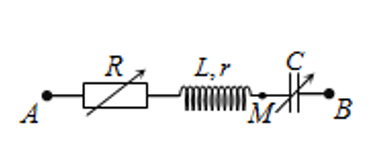
Cho mạch điện xoay chiều như hình vẽ, trong đó giá trị biến trở R và điện dung C của tụ có thể thay đổi được, cuộn dây thuần cảm có độ tự cảm L. Đặt giá trị điện dung $\Large\ C={{C}_{1}}=\dfrac{{{10}^{-4}}}{\pi }$F rồi thay đổi giá trị biến trở R thì nhận thấy điện áp hiệu dụng $\Large\ {{U}_{AM}}$ đạt giá trị nhỏ nhất là $\Large\ {{U}_{1}}$ khi $\Large\ R=0$. Đặt giá trị điện dung $\Large\ C={{C}_{2}}=\dfrac{{{10}^{-3}}}{6\pi }$F rồi thay đổi giá trị biến trở $\Large\ R$ thì nhận thay điện áp hiệu dụng $\Large\ {{U}_{AM}}$ đạt giá trị lớn nhất là $\Large\ {{U}_{2}}=3{{U}_{1}}$ khi $\Large\ R=0$. Biết tần số dòng điện là 50 Hz. Giá trị của độ tự cảm $\Large\ L$ là

• A.

  A. $\Large\ \dfrac{10}{3\pi }$ H

• B.

  B. $\Large\ \dfrac{0,4}{\pi }$ H 

• C.

  C. $\Large\ \dfrac{0,8}{\pi }$ H

• D.

  D. $\Large\ \dfrac{1}{\pi }$ H

+ Ta có $\Large\ {{U}_{AM}}=\dfrac{U\sqrt{{{\left( R+r \right)}^{2}}+Z_{L}^{2}}}{\sqrt{{{\left( R+r \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\dfrac{U}{\sqrt{1+\dfrac{{{Z}_{C}}\left( {{Z}_{C}}-2{{Z}_{L}} \right)}{{{\left( R+r \right)}^{2}}+Z_{L}^{2}}}}$.
Khi $\Large\ {{Z}_{C}}={{Z}_{C1}}=100  \Omega$, thay đổi $\Large\ R$ thì $\Large\ {{U}_{AM\min }}$ khi $\Large\ R=0$, ta thấy rằng để $\Large\ {{U}_{AM\min }}$ thì mẫu số phải lớn nhất, điều này xảy ra tại $\Large\ R=0$ khi $\Large\ {{Z}_{C1}}>2{{Z}_{L}}$ hay $\Large\ {{Z}_{L}}<50 \Omega$.
+ Tương tự như vậy, khi $\Large\ {{Z}_{C}}={{Z}_{C2}}=60 \Omega$ thì $\Large\ {{U}_{AMmax}}$ khi $\Large\ R=0$, ta thấy rằng để $\Large\ {{U}_{AM\max }}$ thì mẫu số phải nhỏ nhất, điều này xảy ra tại $\Large\ R=0$ khi $\Large\ {{Z}_{C2}}<2{{Z}_{L}}$ hay $\Large\ {{Z}_{L}}>30 \Omega$.
Dựa vào khoảng đáp án bài toán, ta thấy $\Large\ L=\dfrac{0,4}{\pi }$H 
→ Đáp án B