Mạch điện nối tiếp AB (như hình 1) với với $\Large\ 0 < R_1 \leqslant

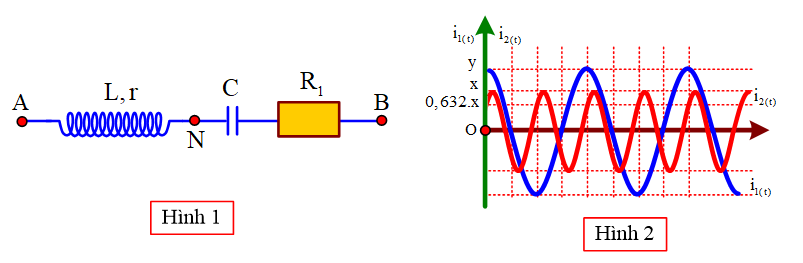
Mạch điện nối tiếp AB (như hình 1) với với $\Large\ 0 < R_1 \leqslant  r$. Mắc AB vào mạng điện xoay chiều có điện áp hiệu dụng không đổi U = 120V nhưng tần số f có thê thay đổi được, ban đầu giữ cho tần số $\Large\ f = f_1$ người ta đo được công suất tiêu thụ trên đoạn NB là $\Large\ P_1$ và cường độ dòng điện $\Large\ i_1(t)$, lúc này nếu nối tắt cuộn dây với tụ điện thì công suất tiêu thụ trên NB lại tăng lên 4 lần. Khi $\Large\ f = f_2$ thì cường độ dòng điện là $\Large\ i_2(t)$. Đồ thị $\Large\ i_1(t)$ và $\Large\ i_2(t)$ được cho (như hình 2). Khi $\Large\ f = f_C$ thì điện áp hiệu dụng hai đầu C đạt cực đại. Tổng giá trị điện áp hiệu dụng $\Large\ U_{AN} + U_{NB}$ khi đó gần giá trị nào nhất?

• A.

  A. 197 (V)

• B.

  B. 195 (V)

• C.

  C. 180 (V)

• D.

  D. 150 (V)

+ Sơ đồ mạch $\Large\ A---L;R---N-{{R}_{1}}-C---B$ 
+ Khi nối tắt cuộn dây, nối tắt tụ $\Large\ \Rightarrow P_{NB}^{/}=\dfrac{{{U}^{2}}}{{{R}_{1}}}$ 
+ Khi không nối tắt: $\Large\ \Rightarrow {{P}_{NB}}=\dfrac{{{U}^{2}}}{\dfrac{{{\left( r+{{R}_{1}} \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}{{{R}_{1}}}}$ 
+ Giải thiết:
 $\Large\ \begin{align}
  & P_{NB}^{/}=4{{P}_{NB}}\Rightarrow \dfrac{{{\left( r+{{R}_{1}} \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}{{{R}_{1}}}=4{{R}_{1}} \\ 
 & \Rightarrow \left( r+{{R}_{1}}-2{{R}_{1}} \right)\left( r+{{R}_{1}}+2{{R}_{1}} \right)+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}=0 \\ 
\end{align}$ 
$\begin{align}
  & \Rightarrow \left( r-{{R}_{1}} \right)\left( R+3{{R}_{1}} \right)+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}=0 \\ 
 & \Rightarrow {{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}=\left( r+3{{R}_{1}} \right)\left( {{R}_{1}}-R \right) \\ 
\end{align}$ 
+ Để tồn tai nghiệm $\Large\ {{R}_{1}}\ge r$ kết hợp với điều kiện $\Large\ {{R}_{1}}\le r\Rightarrow {{R}_{1}}=r;{{Z}_{L1}}={{Z}_{C1}}\Rightarrow {{I}_{1}}$ lớn nhất
+ Khi $\Large\ f = f_2$ nhìn đồ thị ta có: $\Large\ {{T}_{1}}=2{{T}_{2}}\Rightarrow {{f}_{2}}=2{{f}_{1}}\Rightarrow {{Z}_{L2}}=2{{Z}_{L1}};{{Z}_{C2}}=\dfrac{{{Z}_{C1}}}{2}=0,5{{Z}_{L1}}$ 
+ Xét t = 0 $\Large\ \Rightarrow {{\varphi }_{i2}}=-\arccos \left( 0,632 \right)=-0,887;{{\varphi }_{i1}}=0\Rightarrow {{\varphi }_{2}}=0,887\left( rad \right)$ 
$\Large\ \Rightarrow \tan {{\varphi }_{2}}=\dfrac{{{Z}_{L2}}-{{Z}_{C2}}}{{{R}_{td}}}\Rightarrow {{Z}_{L1}}={{Z}_{C1}}=0,82\left( {{R}_{td}} \right)\Rightarrow \dfrac{{{\left( {{R}_{td}} \right)}^{2}}C}{2L}=0,75\left( 1 \right)$ 
+ Khi $\Large\ f = f_c$ thì $\Large\ {{U}_{C\max }}\Rightarrow {{U}_{C\max }}=\dfrac{U}{\sqrt{1-{{\left( 1-\dfrac{{{\left( {{R}_{td}} \right)}^{2}}C}{2L} \right)}^{2}}}}=32\sqrt{15}\left( V \right)$ 
+ Mặt khác $\Large\ U_{C\max }^{2}=U_{L}^{2}+{{U}^{2}}\Rightarrow {{U}_{L}}=8\sqrt{15}\left( V \right)\Rightarrow {{U}_{R}}={{U}_{R1}}=12\sqrt{10}\left( V \right)$ 
$\Large\ \Rightarrow {{U}_{AN}}+{{U}_{NB}}=\sqrt{U_{R}^{2}+U_{L}^{2}}+\sqrt{U_{R1}^{2}+U_{C}^{2}}\approx 179\left( V \right)$ 
→ Đáp án C