Đặt điện áp $\Large\ u=U\sqrt{2}\cos \left( \omega t \right)$ V ($\Lar

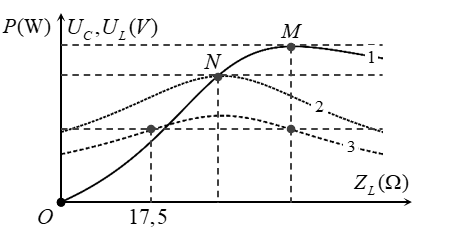
Đặt điện áp $\Large\ u=U\sqrt{2}\cos \left( \omega t \right)$ V ($\Large\ U$ và $\Large\ \omega$ không đổi) vào hai đầu đoạn mạch gồm điện trở có giá trị $\Large\ a \Omega$, tụ điện có điện dung $\Large\ C$ và cuộn thuần cảm có hệ số tự cảm $\Large\ L$ mắc nối tiếp. Biết $\Large\ U=a$ V, $\Large\ L$ thay đổi được. Hình vẽ bên mô tả đồ thị của điện áp hiệu dụng giữa hai bản tụ điện, điện áp hiệu dụng giữa hai đầu cuộn cảm và công suất tiêu thụ điện năng của toàn mạch theo cảm kháng. M và N lần lượt là hai đỉnh của đồ thị (1) và (2). Giá trị của $\Large\ a$ bằng

• A.

  A. 30

• B.

  B. 50

• C.

  C. 40

• D.

  D. 60

+ Từ đồ thị, ta thấy rằng $\Large\ {{Z}_{{{L}_{M}}}}$ là giá trị của cảm kháng để điện áp hiệu dụng trên cuộn dây cực đại  → $\Large\ {{Z}_{{{L}_{M}}}}=\dfrac{{{R}^{2}}+Z_{C}^{2}}{{{Z}_{C}}}$.
+ Tại N mạch xảy ra cộng hưởng, khi đó điện áp hiệu dụng trên tụ là 40 V 
→ $\Large\ {{U}_{C}}=\dfrac{U{{Z}_{C}}}{R}$ ↔ $\Large\ 40=\dfrac{a{{Z}_{C}}}{a}$ → $\Large\ {{Z}_{C}}=40 \Omega$.
+ $\Large\ {{Z}_{L}}=17,5 \Omega$ và $\Large\ {{Z}_{{{L}_{M}}}}$ là hai giá trị của cảm kháng cho cùng công suất tiêu thụ.
→ $\Large\ {{Z}_{{{L}_{M}}}}+17,5=2{{Z}_{C}}$ → $\Large\ {{Z}_{{{L}_{M}}}}=62,5 \Omega$.
+ Thay vào $\Large\ {{Z}_{C}}$ và $\Large\ {{Z}_{{{L}_{M}}}}$ vào phương trình đầu tiên, ta tìm được $\Large\ a=30$ 
→ Đáp án A